线性表

发表于 更新于 阅读次数： 本文字数： 2k 阅读时长 ≈ 2 分钟
数据结构与算法——线性表

线性表

线性表（linear list）：具有相同性质的数据元素顺序排列形成的优先序列

由于顺序存储结构存在以下问题：

  • 存储空间分配不灵活
  • 运算的空间复杂度高

因此，链式存储结构更佳

顺序表——线性表的顺序存储方式

顺序表有以下特点：
数据元素依次顺序存储在一组连续的存储单元中，知道某个元素的位置就可以计算其他元素，获得任意元素的复杂度为$O(1)$
数据元素的物理存放顺序与其逻辑顺序一致

顺序表的查找操作

顺序查找的ASL（Average Search Length）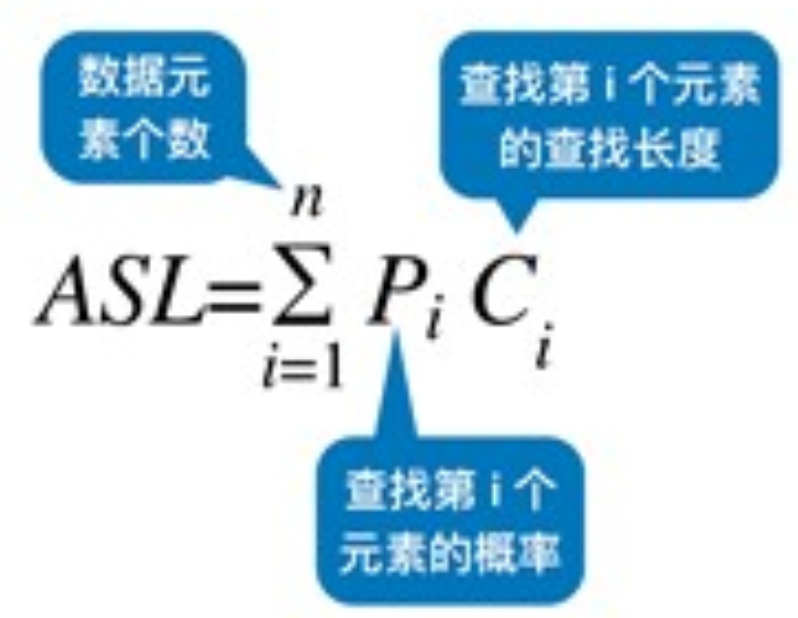
alt text
假设每个元素查找的概率相等：$P_i = 1/n$
则$ASL =（1 + 2 + 3 +…+n）/ n = (n + 1) / 2$
时间复杂度为$O(n)$

顺序表的插入操作

算法步骤：

  1. 判断插入位置是否合法
  2. 判断顺序表的存储空间是否已满，已满则返回False
  3. 空出第 i 个位置，将第 n 至第 i 位的元素依次向后移动一个位置
  4. 将要插入的新元素放入第 i 个位置
  5. 表长加一

复杂度分析：

  1. 在第 i 个位置插入元素的先验概率$P_i = 1 / n + 1$
  2. 则期望为：
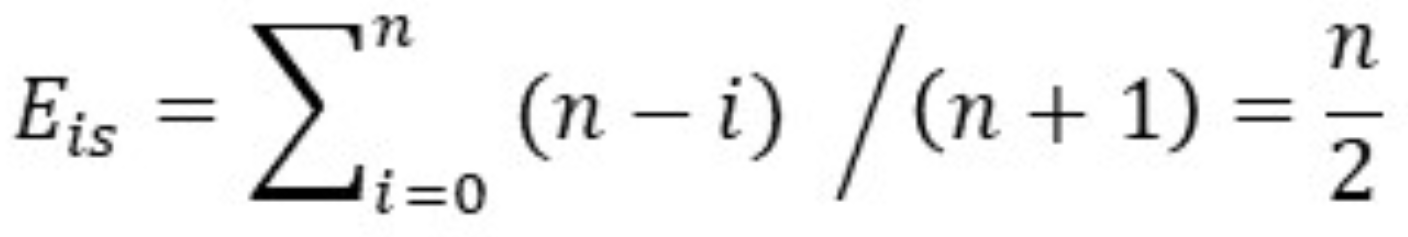
    alt text

插入一个元素的平均时间复杂度为$O(n)$

顺序表的删除操作

算法步骤：

  1. 判断插入位置是否合法
  2. 将待删除的元素保留
  3. 空出第 i + 1 个位置至第 n 位的元素依次向前移动一个位置
  4. 表长减一

复杂度分析：

  1. 在第 i 个位置删除元素的先验概率$P_i = 1 / n$
  2. 共有 n - i - 1 个元素需要移动
  3. 则期望为：
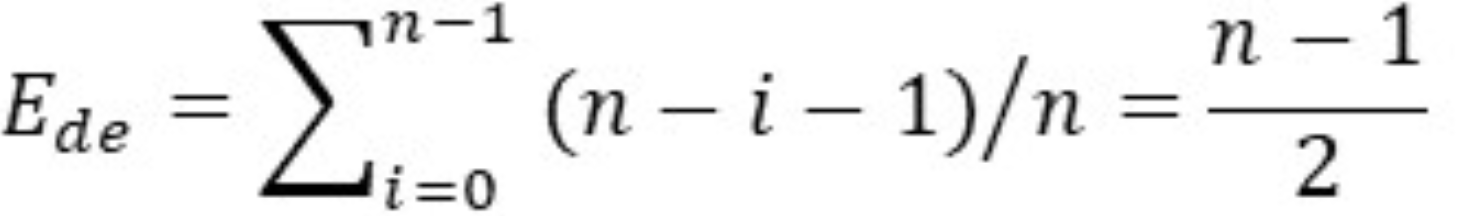
    alt text
    删除一个元素的平均时间复杂度为$O(n)$

顺序表的优缺点

  • 可以直接访问表中的元素
  • 插入/删除操作设计大量元素移动，复杂度高
  • 静态存储，不可扩充

单向链表——线性表的链式存储方式

单向链表表有以下特点：
存储单元可以不连续
用额外的存储空间存放数据元素的逻辑位置
采用指针链接逻辑相邻的元素

在链表中插入新节点

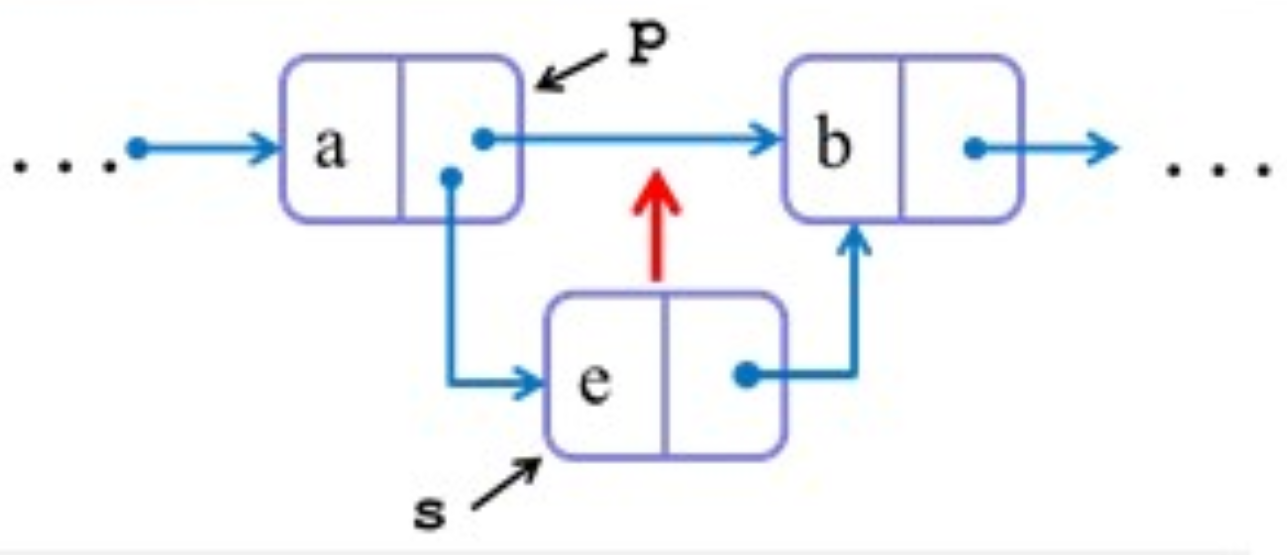
alt text
步骤：

  1. s -> next = p -> next
  2. p -> next = s

颠倒顺序会导致自循环

在链表中删除节点

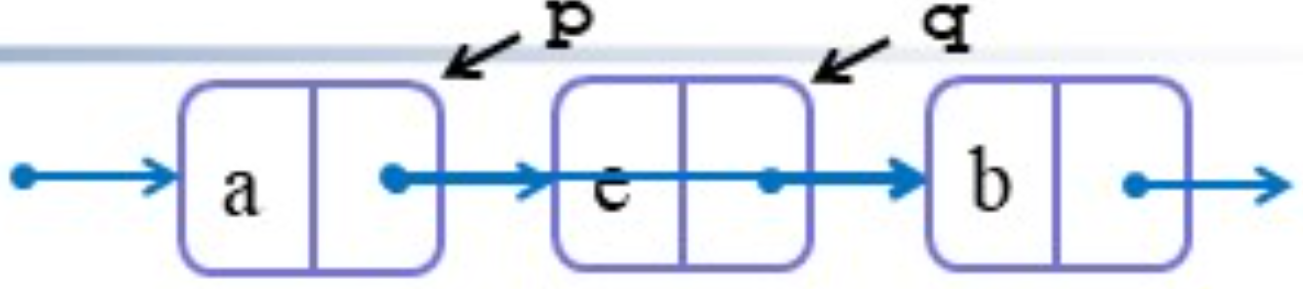
alt text
步骤：

  1. q = p -> next
  2. p -> next = q -> next
  3. delete q; q = null

定义SeqList和LinkList均继承自LinearLis出现的问题

alt text

使用引用传递可以避免对象切割，防止破坏多态性：
alt text

Slicing Problem 对象切割问题

产生原因：

  • 当把一个派生类对象赋给一个基类对象时（并不是使用父类指针或引用接收子类对象），会发生对象切割。(另外用基类对象强制转换派生类对象也会)
    alt text

  • 接收值传递的返回值时，发生的拷贝构造也会发生对象切割
    alt text

发生对象切片后派生类的覆盖部分就被切掉了，所以调用的方法将会是父类方法

与对象切割类似的，还有静态联编问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
//基类
class Base{
public:
	 void printError(){  //使用virtual关键字声明函数，将其变为虚函数，即可使用多态
	 cout << "基类方法!" << endl;
	 };
};
//派生类
class Derived : public Base{
public:
	 void printError(){
		cout << "派生类方法!" << endl;
	}
};
void test()
{	
	Base *ex = new Derived(); //静态联编导致子类对象调用基类方法，而不是子类方法
	ex->printError(); //输出基类方法！
}
int main()
{
   test();
   return 0;
}

静态联编行为：
当基类函数未声明为virtual时，编译器根据指针/引用的静态类型（声明类型）
决定调用哪个函数。
示例中Base* ex的静态类型是Base*，因此ex->printError()直接调用Base::printError()，即使对象实际是Derived类型。

单向链表的特点：

  1. 可以灵活改变长度
  2. 插入/删除无需移动大量数据
  3. 通过指针表示数据间的顺序关系
  4. 表长需要遍历获取
  5. 插入/删除操作中寻找相应位置的复杂度高

双向链表——增加前驱指针的单向链表

alt text
对于单向链表，想要获取后继元素，复杂度为$O(1)$,但是想要获取前驱元素，需要遍历，复杂度为$O(n)$
双向链表使得两个操作的复杂度都为$O(1)$

双向链表的插入操作

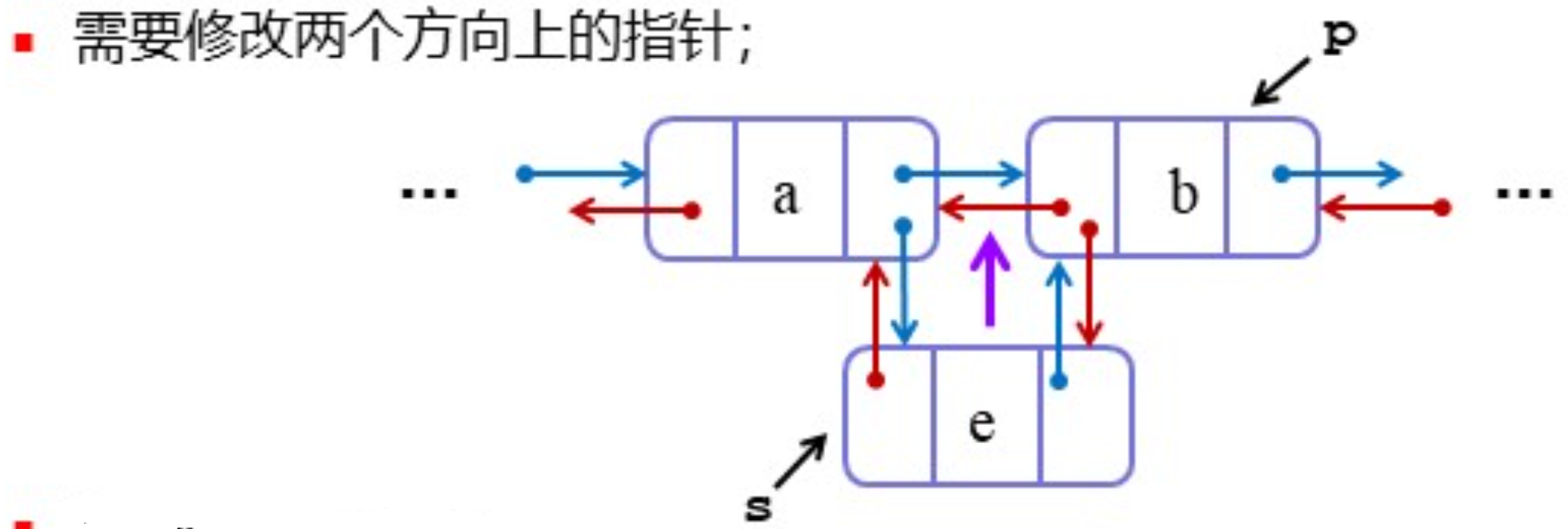
alt text

算法步骤：

  • 让前驱指向s：

  • p -> prev -> next = s

  • 以s为中心，设置它的前驱后继

  • s -> next = p

  • s -> prev = p -> prev

  • 让后继指向s

  • p -> prev = s

双向链表的删除操作

alt text

算法步骤：

  • 让p的前驱向后指：

  • p -> prev -> next = p -> next

  • 让p的后继向前指：

  • p -> next -> prev = p -> prev

  • 删除p

  • delete p