栈和队列

发表于 更新于 阅读次数： 本文字数： 3.6k 阅读时长 ≈ 3 分钟
数据结构与算法——栈和队列

栈和队列

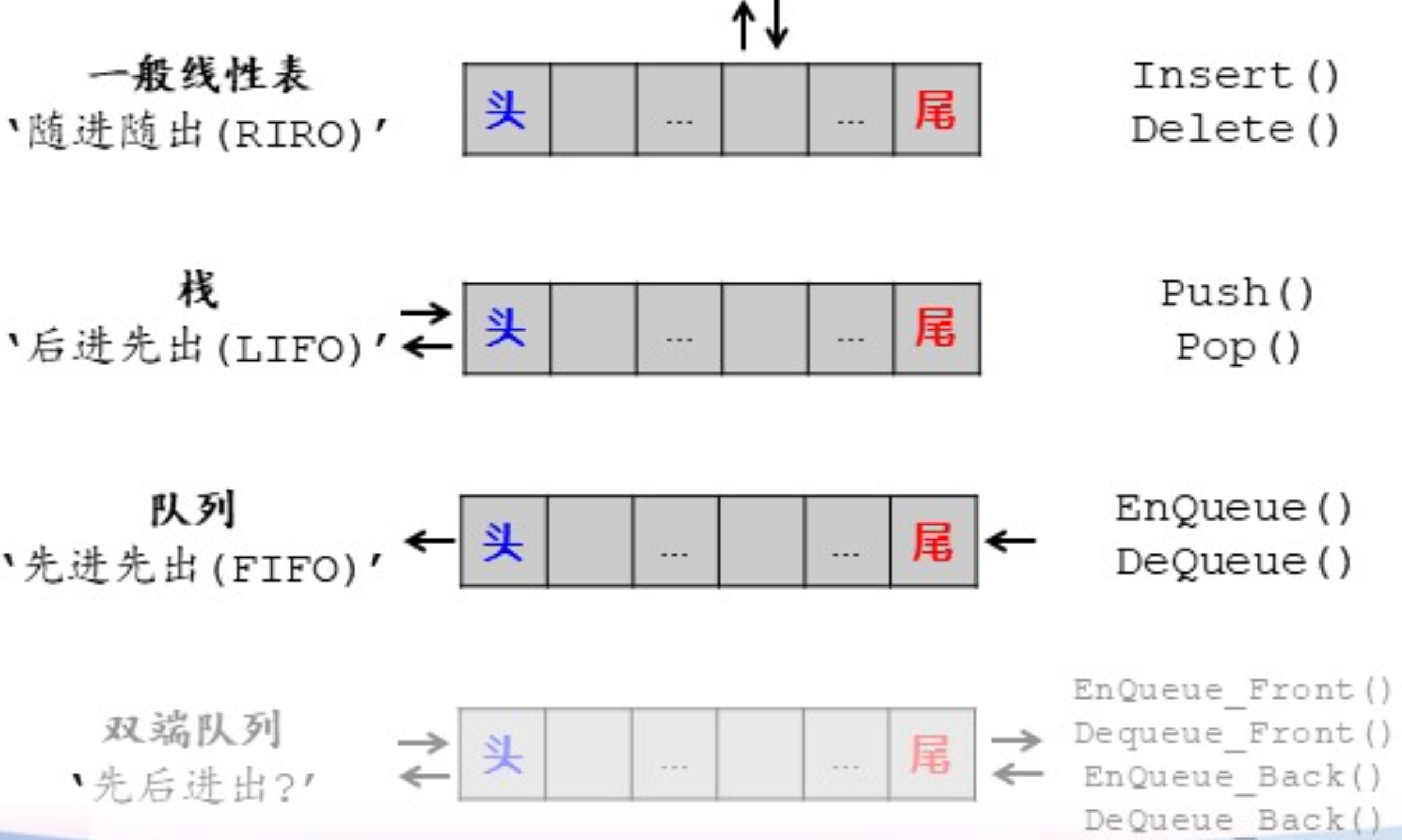
栈、队列、双端队列均是线性表的特殊情况（访问受限的线性表）

alt text

栈

  • 允许插入、删除的一端称为栈顶(top)，另一端称为栈底(bottom)
  • 在栈顶插入元素称为入栈(push)，删除元素称为出栈(pop)

顺序栈——栈的顺序存储实现

顺序栈存储空间的处理
alt text

顺序栈的特点：

  1. 顺序栈的入栈和出栈、构造和销毁的复杂度都是$O(1)$
  2. 可以采用溢出时增容，或者共享栈的方式提高空间利用率

链式栈——栈的链式存储分配实现

链式栈的特点：

  1. 链式栈的入栈和出栈复杂度为$O(1)$，构造和销毁的复杂度是$O(n)$(需要逐个释放/创建)
  2. 栈的长度动态变化，空间利用率高，一般无需判断溢出

栈的应用

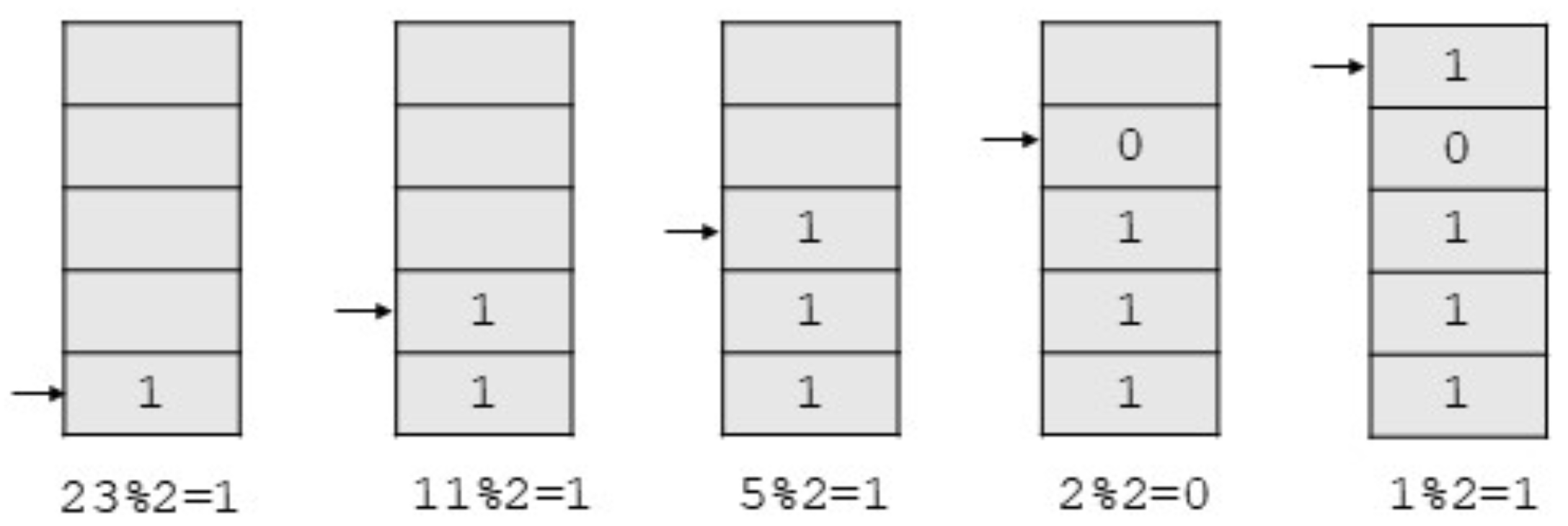
  • 十进制数到二进制数的转换
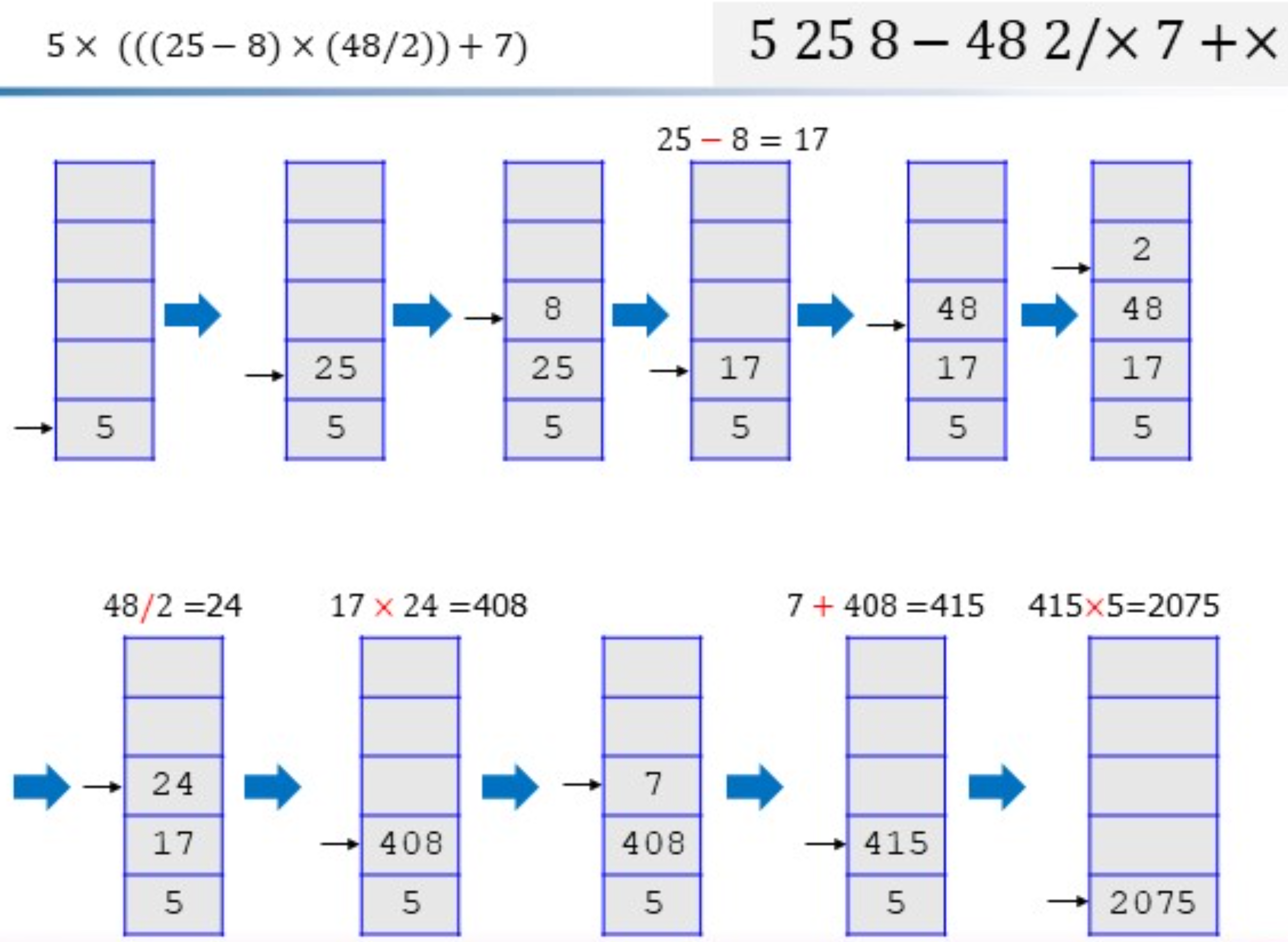
    alt text

  • 算术表达式求值的栈实现

    中缀表达式实现步骤：

    1. 初始化:结束符‘#’入栈：Sr.Push(‘#’)
    2. 如果W是操作数则入栈：Sd.Push(W)
    3. 若W为运算符，则有以下几种情况:
      1. 若W优先级高于Sr栈顶元素则入栈：Sr.Push(W)
      2. 若W优先级低于Sr栈顶元素则执行运算操作:
        Sd.Pop(x1);
        Sd.Pop(x2);
        Sr.Pop(@);
        Sd.Push(x2@X1);
      3. 若W等于Sr栈顶元素则弹出Sr栈顶元素

    4. Sd即为运算结果

      中缀转后缀表达式：
      维护两个栈：运算符(OP)和结果栈(R)

    • 扫描到操作数，R入栈;扫描到’(‘，OP入栈
    • 扫描到运算符:
      当前运算符优先级高于OP栈顶元紊优先级，OP入栈
      否则，则OP栈出栈，R栈入栈
    • 扫描到’)’，OP出栈，到pop出’)’为止。如果pop出的元素不是’(‘或’)’，则将元素压入R
      alt text

递归

适用情况：问题可以收敛

  • 阶乘求值
    alt text



  • 阿克曼函数
    特点：随着输入值的增加，函数的值增长得非常快
    定义如下：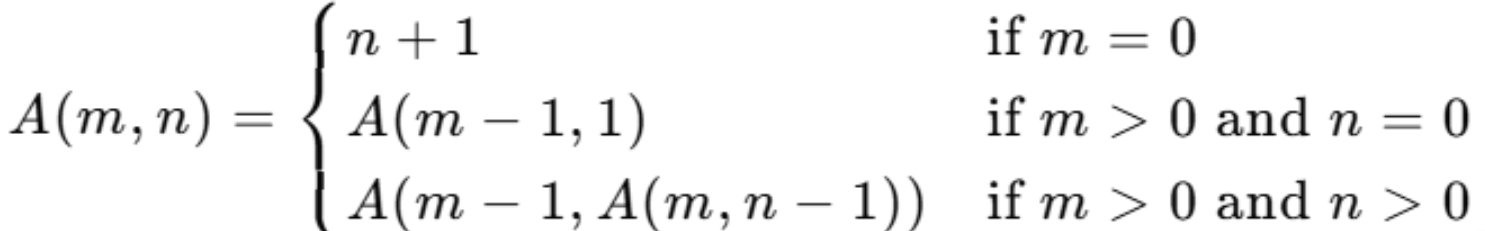
    alt text
    递归实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    #include<bits/stdc++.h>
    using namespace std;
    int c(int m, int n) {
        if(m == 0) return n + 1;
        if(n == 0 && m > 0) return c(m - 1, 1);
        if(m > 0 && n > 0)return c(m - 1, c(m, n - 1));
    }

    int main() {
        int a, b;
        cin >> a >> b;
        cout << c(a, b);
        
        return 0;
    }




  • 斐波那契数列
    递归定义：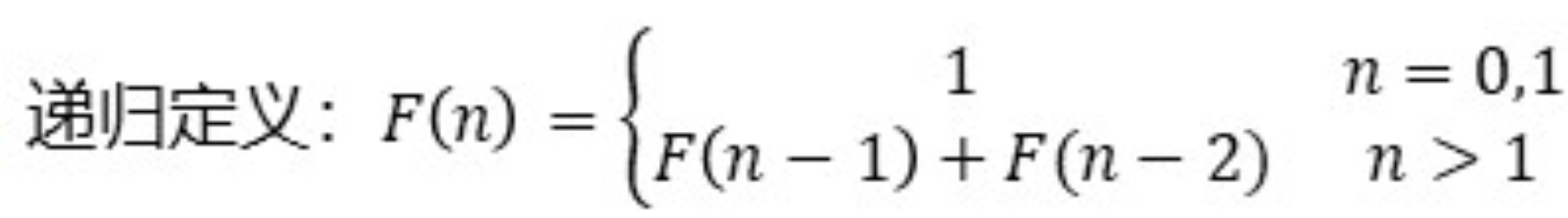
    alt text

    递归实现：
    alt text
    F(5)的栈调用情况：
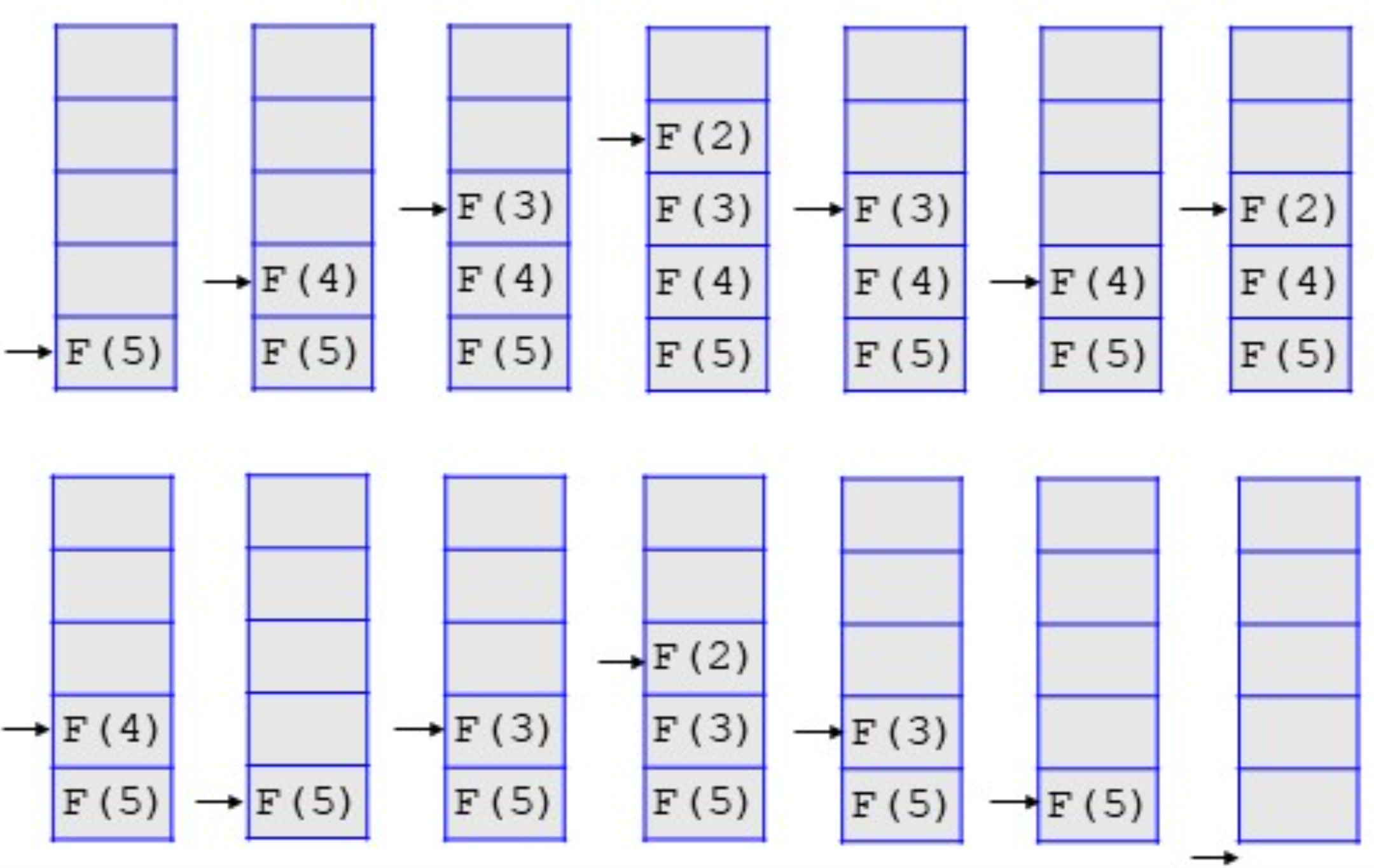
    alt text



  • 最大公约数
    定义：可以同时除尽两个正整数的最大的正整数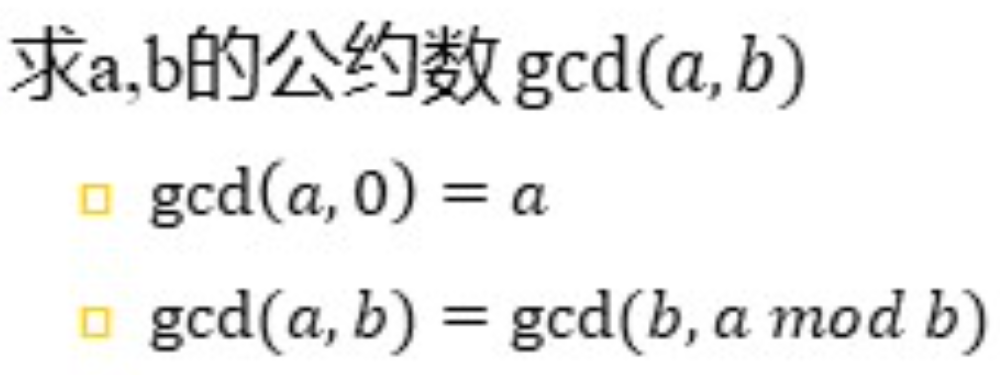
    alt text

    递归实现：

    1
    2
    3
    4
    5
    6
    long gcd(unsigned long a,unsigned long b)
    {
        int r = a % b;
        if(r != 0) return gcd(b，r);
        else return b;
    }




  • 互递归
    定义：一种非直接递归，两个函数互相借助对方定义
    示例：
    alt text



  • 汉诺塔问题
    递归步骤：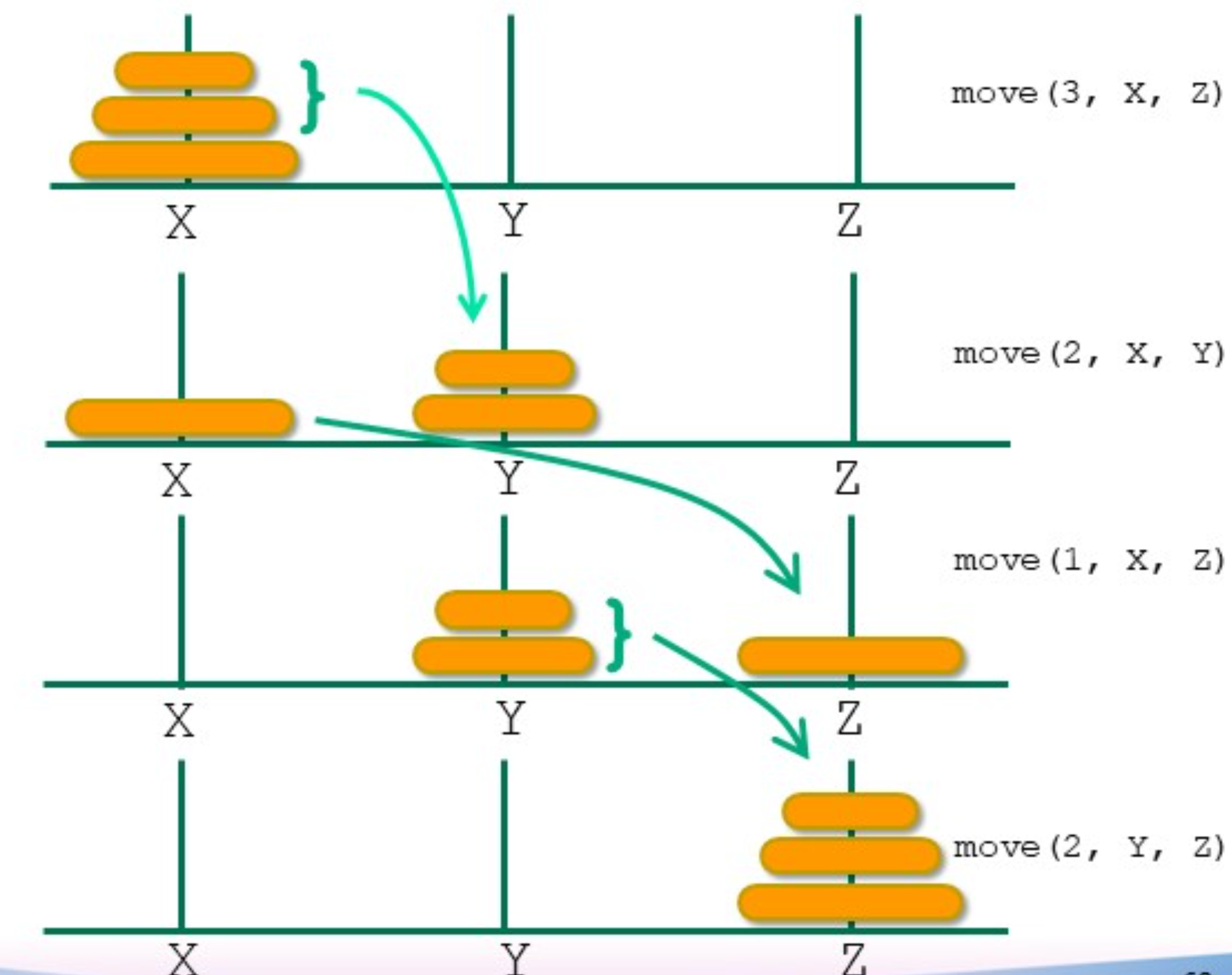
    alt text

    递归实现：
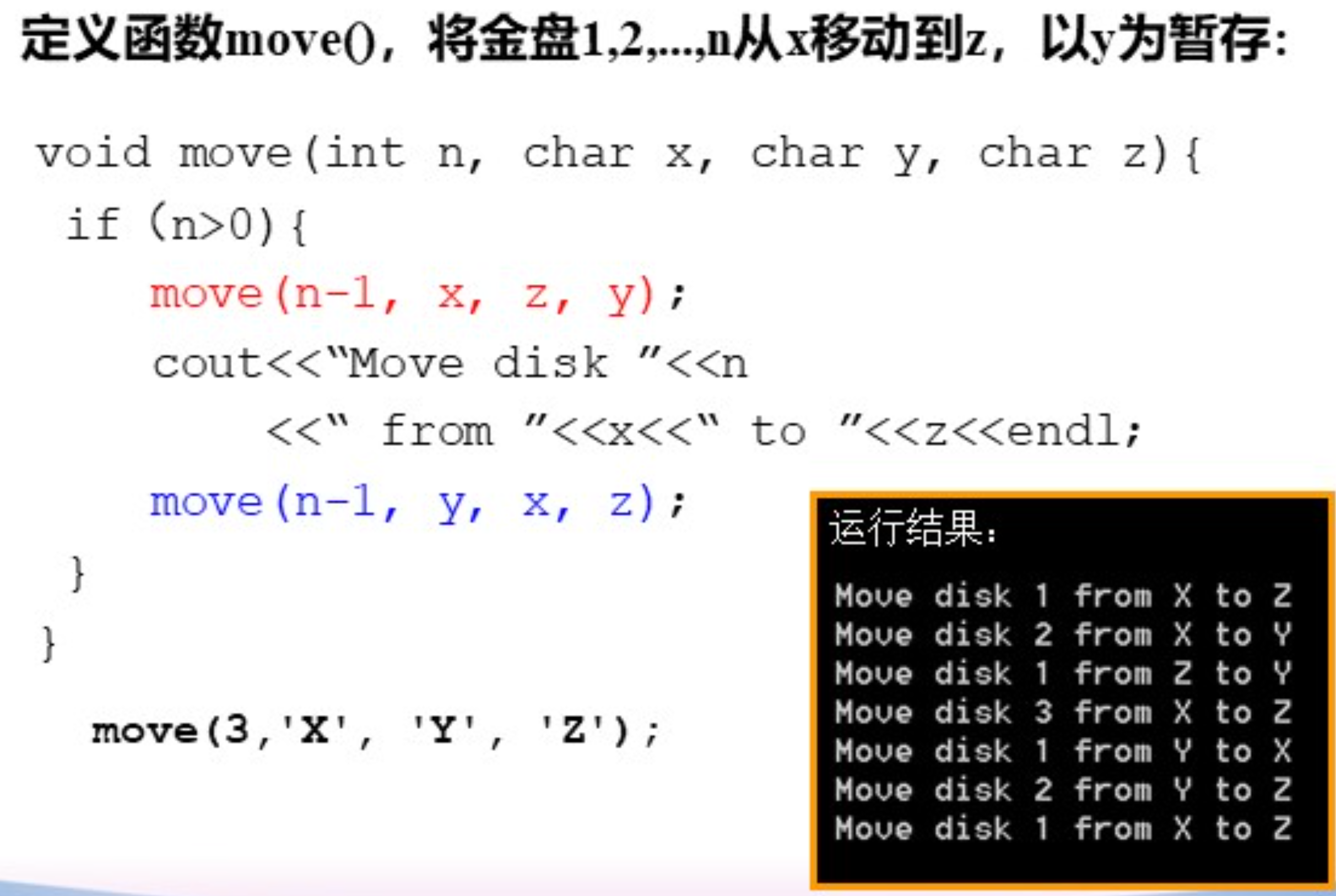
    alt text
    先把 n - 1 个移动到y，然后移动最底下的到z，然后把 n - 1 个从y移动到z

    复杂度分析：
    alt text



递归的消去

尾递归

定义：函数最后操作时递归调用或平凡返回（返回已经存在的值）

为什么需要尾递归？
对于非尾递归来说，由于最后的返回值需要额外计算，因此经历了创建栈帧、销毁栈帧的过程，可能导致栈溢出。

以计算阶乘的普通递归实现为例:

1
2
3
4
5
6
int factorial(int n) {
   if (n == 0)
       return 1;
   else
       return n * factorial(n - 1);
}

当调用factorial(3)时，执行过程如下：

调用factorial(3)，创建栈帧A，保存参数n=3。
执行到return n * factorial(n - 1)时，需要先计算factorial(2)的值。

调用factorial(2)，创建新的栈帧B，保存参数n=2。
执行到return n * factorial(n - 1)时，需要先计算factorial(1)的值。

调用factorial(1)，创建新的栈帧C，保存参数n=1。
执行到return n * factorial(n - 1)时，需要先计算factorial(0)的值。

调用factorial(0)，创建新的栈帧D，保存参数n=0。
执行到return 1，返回值1，销毁栈帧D。

栈帧C继续执行，计算1 1=1，返回值1，销毁栈帧C。
栈帧B继续执行，计算2 1=2，返回值2，销毁栈帧B。
栈帧A继续执行，计算3 * 2=6，返回值6，销毁栈帧A。

在这个过程中，每次递归调用都会创建新的栈帧，栈帧数量随着递归深度增加而增加，可能导致栈溢出，并且每次创建和销毁栈帧都会带来性能开销。


尾递归优化的执行过程：

1
2
3
4
5
6
int factorial_tail(int n, int acc) {
    if (n == 0)
        return acc;
    else
        return factorial_tail(n - 1, n * acc);
}

初始调用时，acc的初始值为1。例如，计算factorial_tail(3, 1)的执行过程如下：
调用factorial_tail(3, 1)，创建栈帧A，保存参数n=3，acc=1。

执行到return factorial_tail(n - 1, n * acc)时，计算新的参数值n-1=2，$nacc=31=3$。
调用factorial_tail(2, 3)，复用栈帧A，更新参数n=2，acc=3。

执行到return factorial_tail(n - 1, n * acc)时，计算新的参数值n-1=1，$nacc=23=6$。
调用factorial_tail(1, 6)，复用栈帧A，更新参数n=1，acc=6。

执行到return factorial_tail(n - 1, n * acc)时，计算新的参数值n-1=0，$nacc=16=6$。
调用factorial_tail(0, 6)，复用栈帧A，更新参数n=0，acc=6。

执行到return acc，返回值6，销毁栈帧A。

在这个过程中，每次递归调用复用当前栈帧，不需要创建新的栈帧，因此栈帧数量始终保持为1，不会导致栈溢出，并且避免了创建和销毁栈帧的性能开销。

底层原理
尾递归优化的关键在于编译器能够识别出尾递归调用，并将其转换为循环操作。具体来说，当编译器检测到一个函数调用是尾递归时，它会生成代码来复用当前的栈帧，而不是创建新的栈帧。这通常是通过将递归调用的参数更新到当前栈帧的变量中，并跳转到函数的开头重新执行来实现的。

常见简单问题的尾递归实现

1
//TODO...




队列

定义：限制数据一端插入，另一端删除的特殊线性表

  • 允许插入的一端称为队尾(rear)，允许删除的一端称为队头(front)
  • 入队为Enqueue，出队为Dequeue

顺序队列

存储

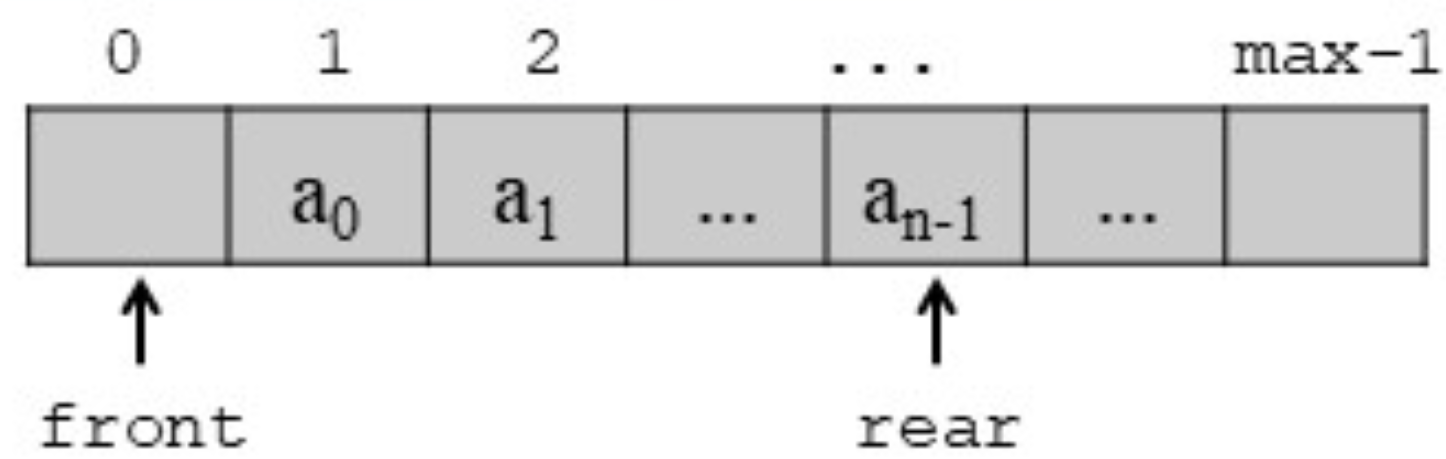
alt text

操作

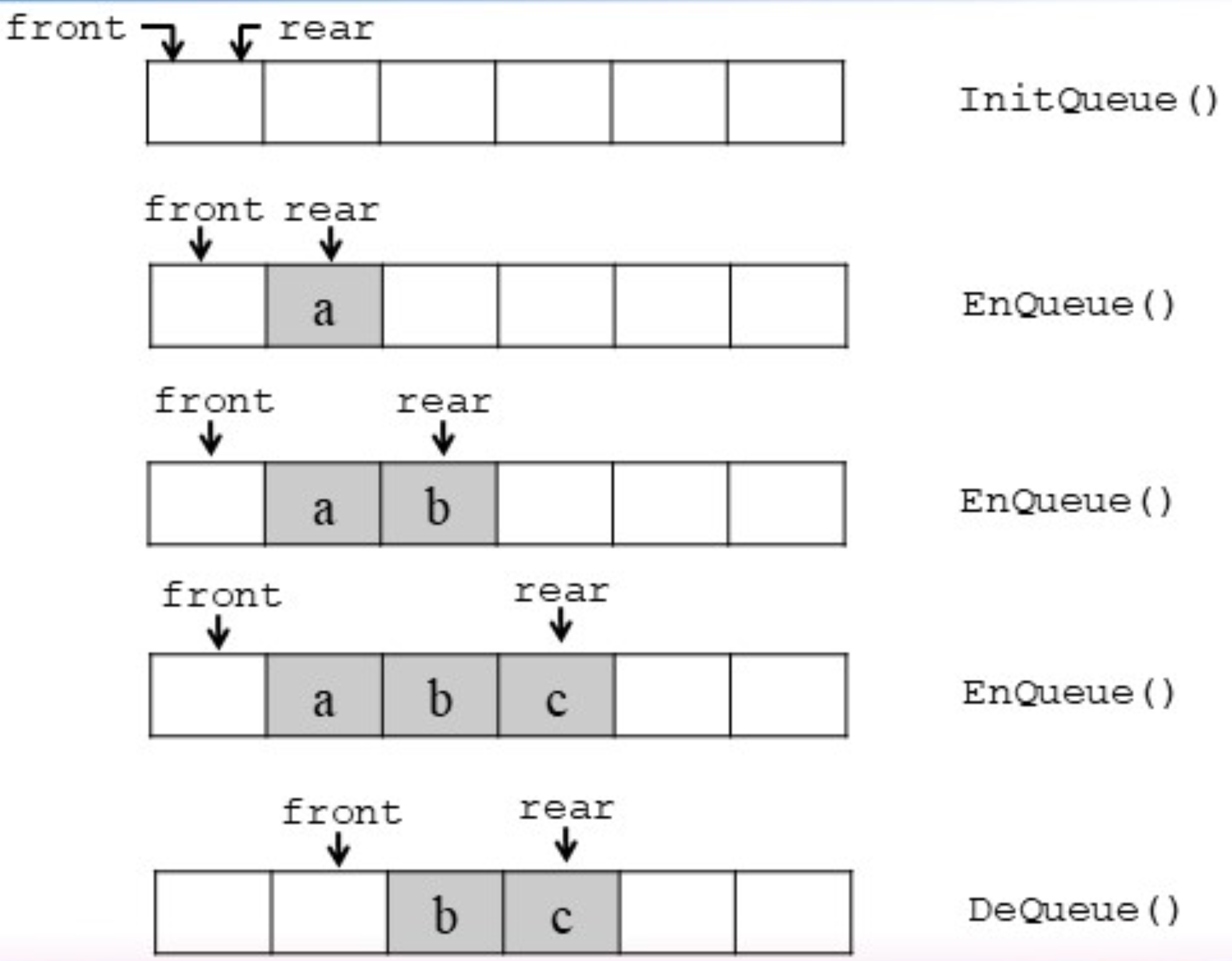
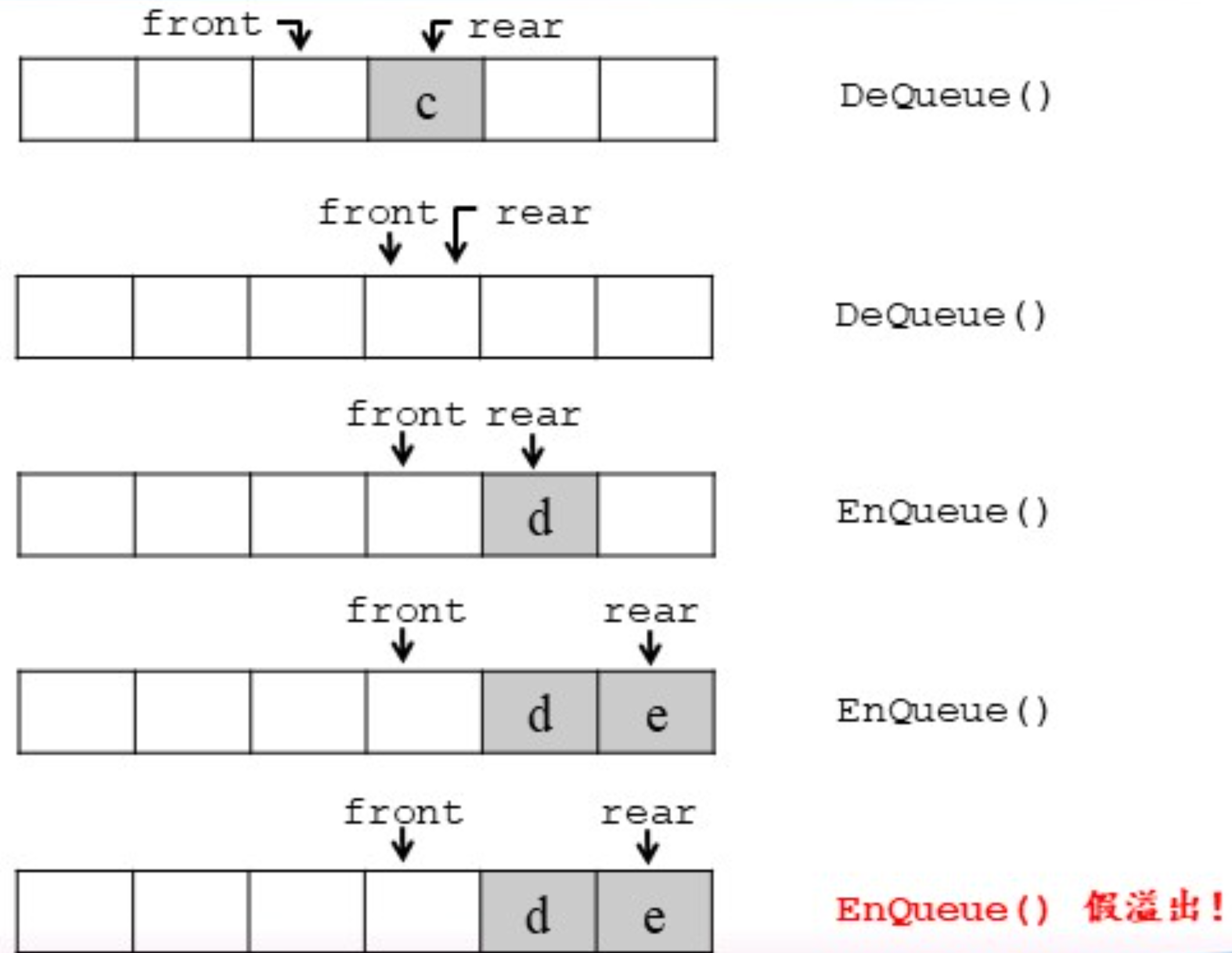
alt text
alt text
假溢出：rear已经到达数组末尾，尽管队列中仍有空闲空间（front之前的位置），但由于rear无法继续向后移动，导致假溢出。

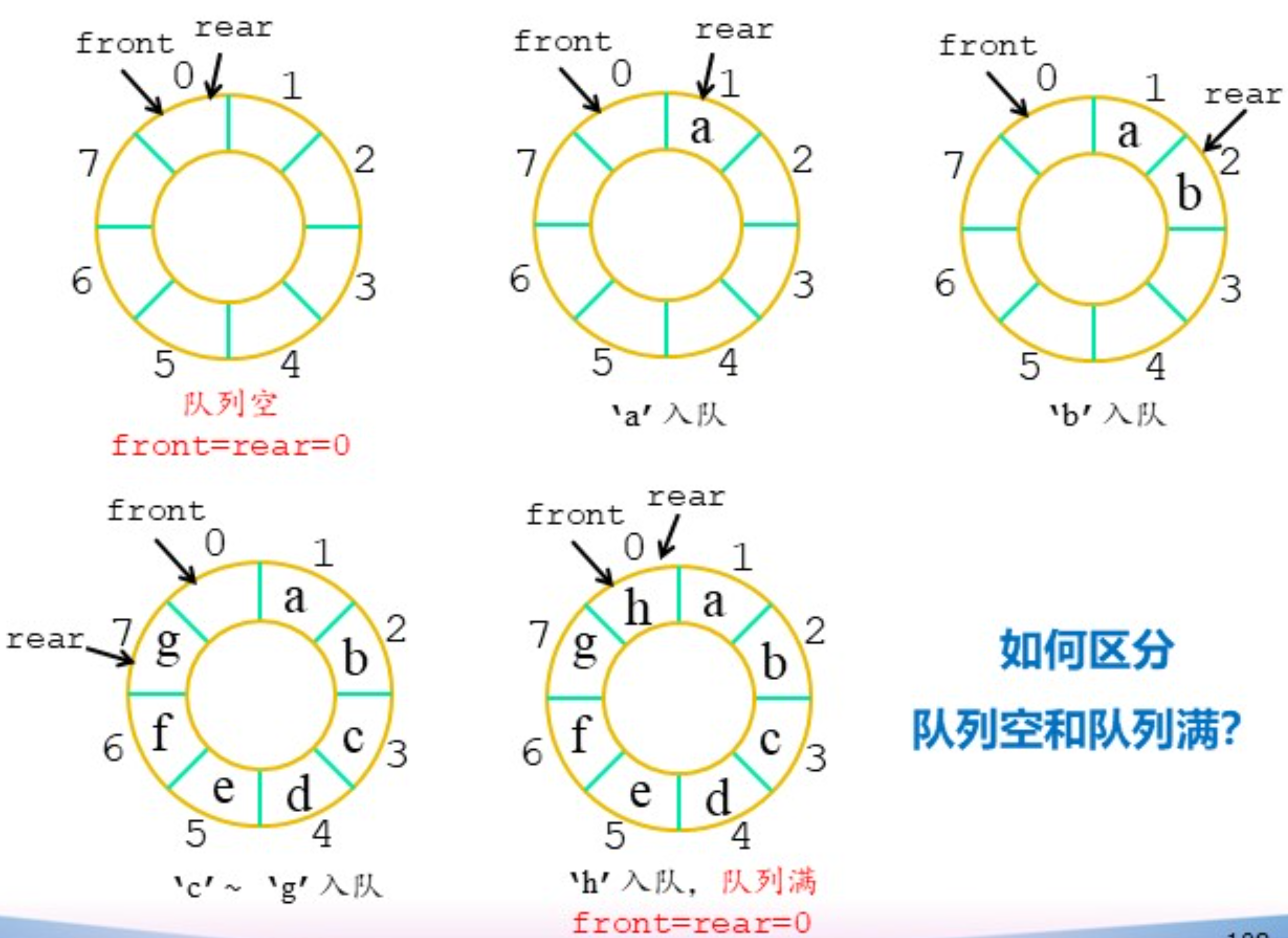
循环队列——解决假溢出问题

顺序数列无法利用队头指针之前的空间，因此假溢出的本质是没有完全利用数组空间。而循环数列通过连成环解决了这一问题。由于首尾相接，因此循环队列需要做的只是找到判空和判满的办法。


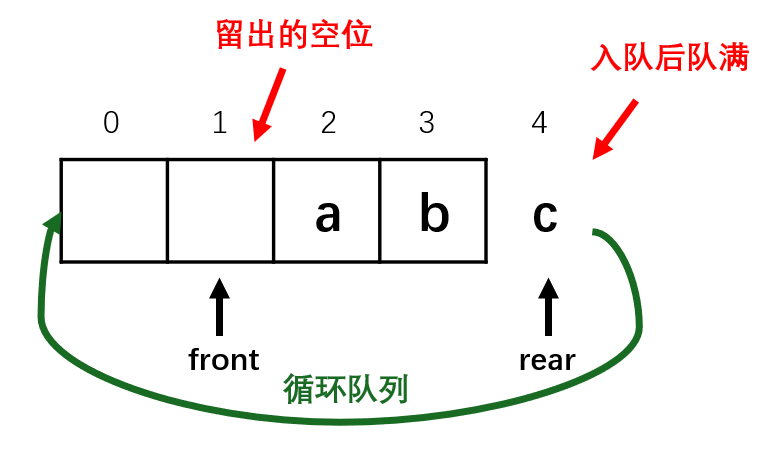
alt text


  • 方法一：留出空位
    alt text
    判断条件：

    1. 队列为空：front == rear
    2. 队列为满：front == (rear + 1) % max

  • 其他方法易于理解：
    alt text



链式队列——链式存储方式

和链表的逻辑一致，易于理解：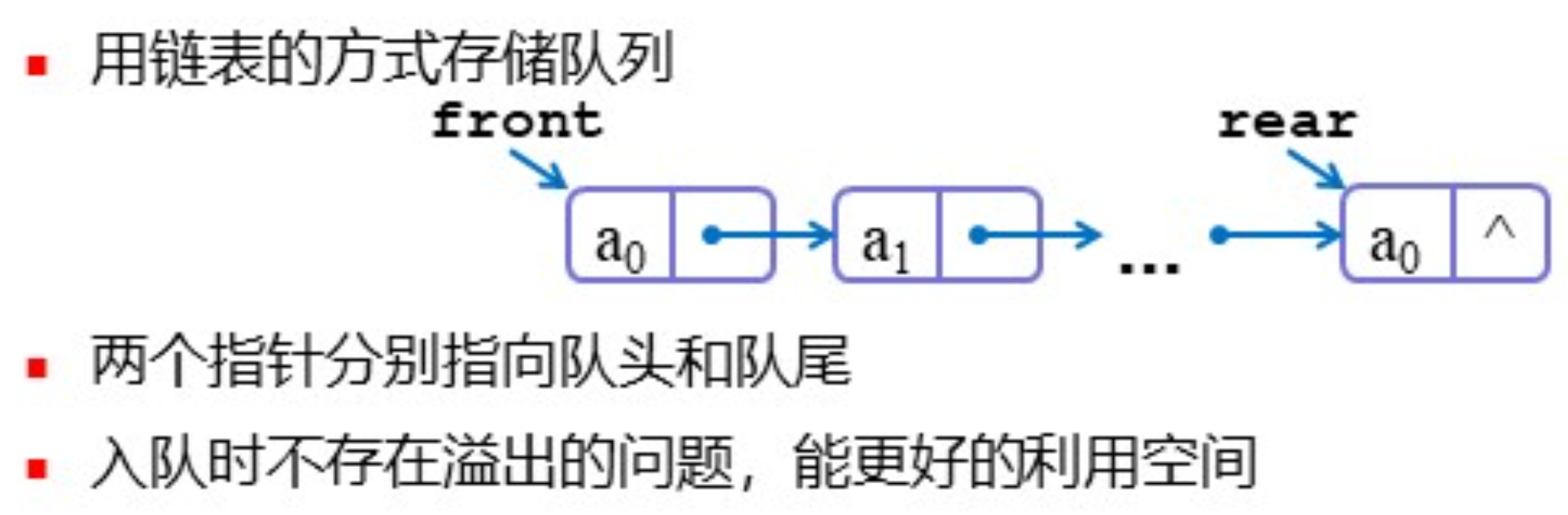
alt text

优先队列

易于理解：
alt text

队列的应用：杨辉三角

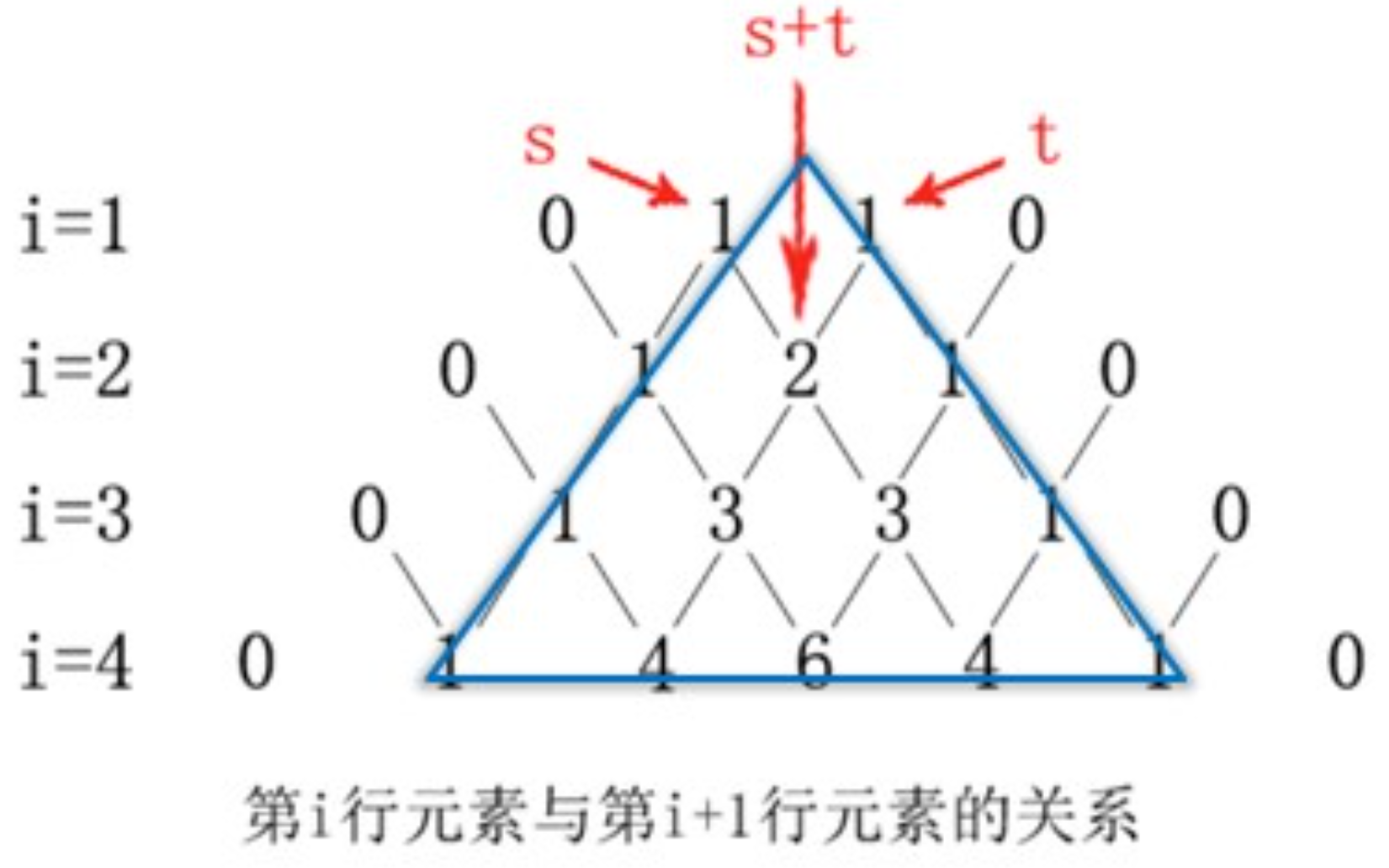
alt text

具体实现：

先进队一个1

此时队列： 1 （这样我们就得到了杨辉三角的第一行）


第一步：在队尾进队一个1

此时队列：1 1

循环0次（这里相当于没有进行操作）（看不懂就往下看）

此时队列：1 1

在队尾进队一个1

1 1 1

出队队头的一个1

1 1 （这样我们就得到了杨辉三角的第二行）

（这里看不懂没关系，接着看就懂了）



第二步：在队尾进队一个1（与第一步中相同操作）

1 1 1

循环一次：进队队头两个元素的和（1+1=2），即进队2；

1 1 1 2

再出队队头的一个元素（1）。这两个操作为一次循环。

1 1 2

在队尾进队一个1（与第一步中相同操作）

1 1 2 1

出队队头的一个1

1 2 1 （这样我们就得到了杨辉三角的第三行）




第三步：

在队尾进队一个1（与第一步中相同操作）

1 2 1 1

循环两次：第一次进队队头两个元素的和（1+2=3），即进队3；

1 2 1 1 3

再出队队头的一个元素（1）。这两个操作为一次循环。

2 1 1 3

第二次再进队队头两个元素的和（2+1=3），即进队3；

2 1 1 3 3

再出队队头的一个元素（2）。这两个操作为第二次循环。

1 1 3 3

在队尾进队一个1（与第一步中相同操作）

1 1 3 3 1

出队队头的一个1

1 3 3 1 （这样我们就得到了杨辉三角的第四行）


经过上面的三步操作，不难看出，每一步都分为三个部分。即：进1；循环；进1出1。所以我们可以控制重复上述步骤的次数，打印出想要的杨辉三角的层数。（并且可以看出，第一步循环0次；第二步循环1次；第三步循环2次。即循环次数为步数-1）


双栈实现队列

1
//TODO...