树与二叉树
树与二叉树
定义
树(Tree)是n(n ≥ 0)个节点的有限集
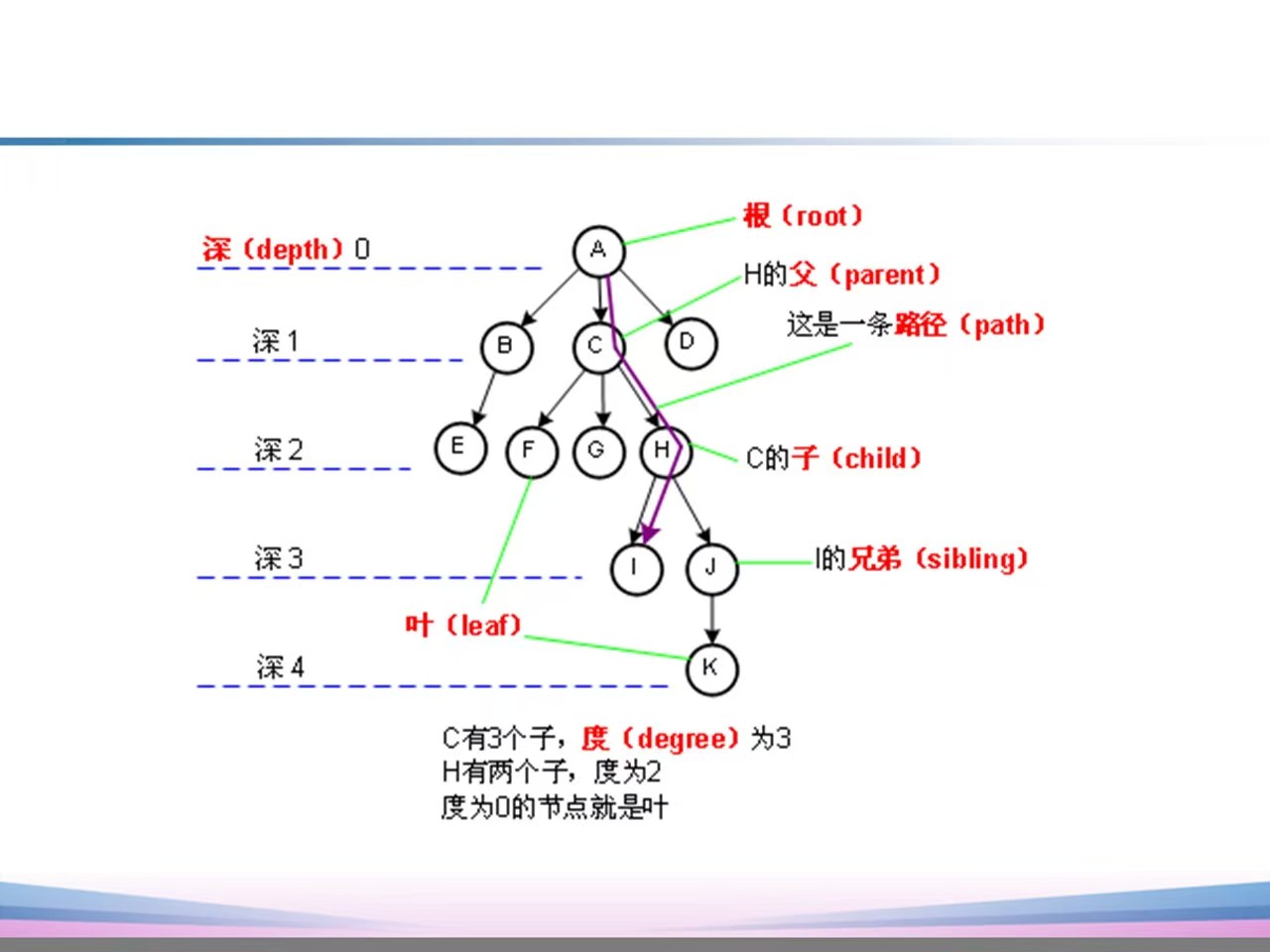
树的基本概念
- 节点的度:每个节点拥有子树的数目(后继的个数)
- 叶子节点:度为0的节点(没有后继的节点)
- 父节点:具有相同的父节点的节点
- 路径:任意两个节点是父子关系
- 树的度:树中节点度最大的值
- 树的深度:树中节点的最大层次
- 祖先节点:某节点到根节点的路径上所有的节点都是该节点的祖先节点
- 森林:m(m ≥ 0)课互不相交树的集合
树的基本性质
性质一:节点数等于节点的度的总和加一
性质二:度为 k 的树,第 i 层至多有 $k^i - 1$ 个节点
性质三:度为 k 且深度为 h 的树至多有 $(k^h - 1)/(k - 1)$ 个节点
性质四:具有 n 个节点的度为 k 的树的最小深度为 $[log_k(n(k -1) + 1)]$ (向上取整)
其他性质:
- 边数等于度数之和
- 边数等于节点数减一
二叉树
定义
二叉树(Binary Tree)是n(n ≥ 0)个节点的有限集
有且只有一个根节点,L称为左子树,R称为右子树,两者不能互换位置。
二叉树每个节点最多有两个孩子
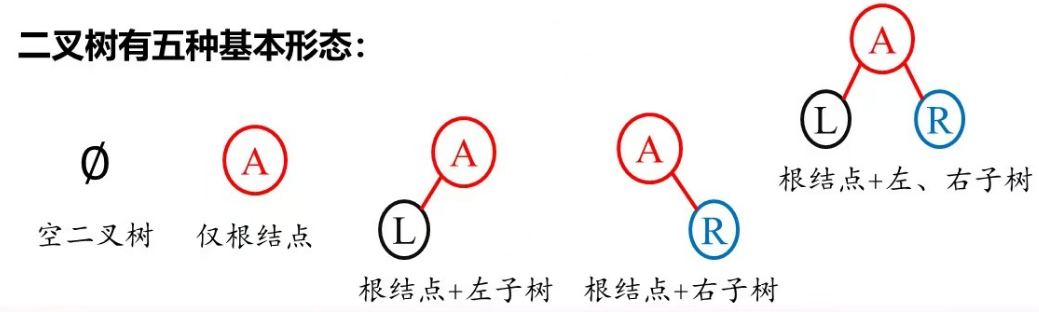
二叉树仅有五种基本形态:
注意:
- 二叉树并不是树的特殊情况,两者是并列的
- 二叉树不是度为2的树,因为二叉树可以是空树,而度为2的树不可以
二叉树的基本性质
- 性质一:第 i 层至多有 $2^{i-1}$ 个节点
性质二:深度为 h 的二叉树至多有 $2^h - 1$ 个节点(跟树的性质三类似)
满二叉树和完全二叉树
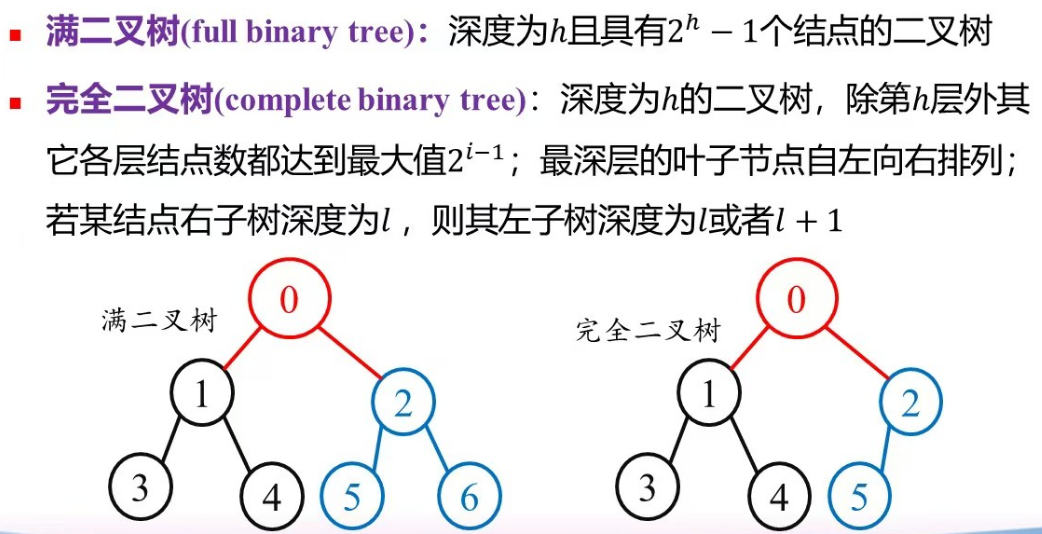
完全二叉树不能只有右孩子性质三:任何非空二叉树,叶子节点数为 $n_0$ ,度为 2 的节点数为 $n_2$ ,则一定有:$n_0 = n_2 + 1$
- 性质四:具有 n 个节点的完全二叉树的深度为 $[ log_2(n + 1) ]$ (向上取整)(跟树的性质四类似)
节点数相同的二叉树中,完全二叉树具有最小深度 - 性质五:对具有 n 个节点的完全二叉树的节点进行自上而下,每层自左向右的编号0,1,2,…,n-1,则有:
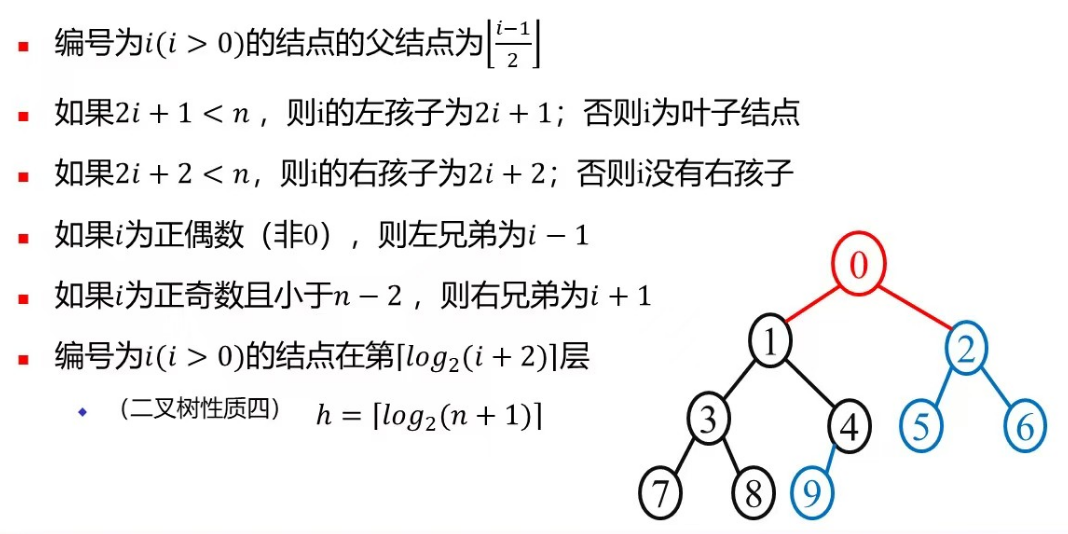
二叉树的存储结构
顺序存储
- 对二叉树节点从上到下,每层从左到右顺序编号
- 按照编号顺序将节点数据元素放入数组
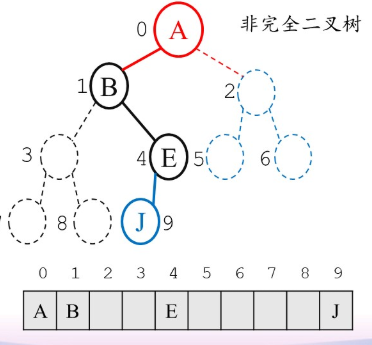
特点:
- 节点间关系蕴含在其存储位置中
- 浪费空间,更用于满二叉树和完全二叉树。仅有 h 个节点的深度为 h 的二叉树空间利用率最低:$h/(2^h - 1)$
链式存储
二叉链表:每个节点包含数据域,左孩子指针域和右孩子指针域
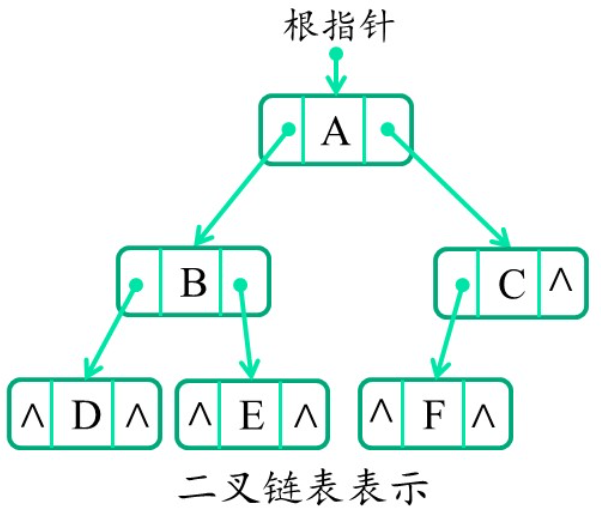
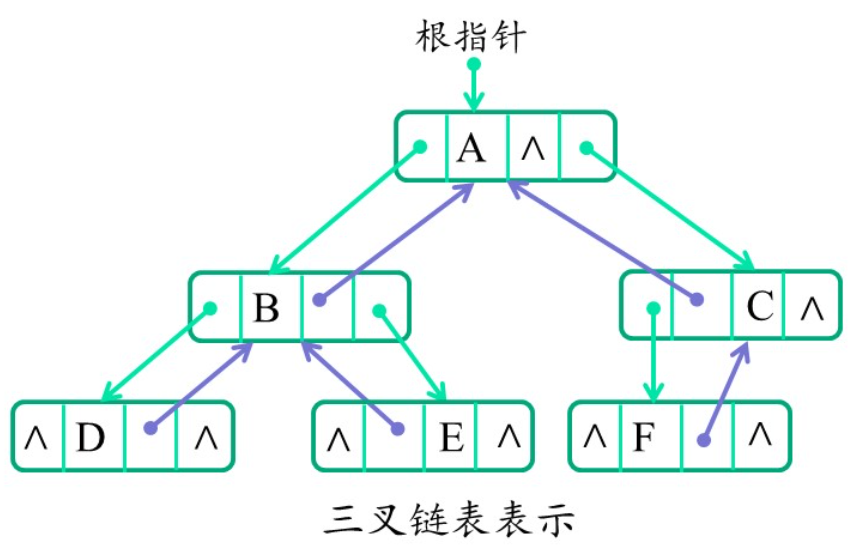
三叉链表:节点增加一个存放指向父节点的指针
二叉树的遍历
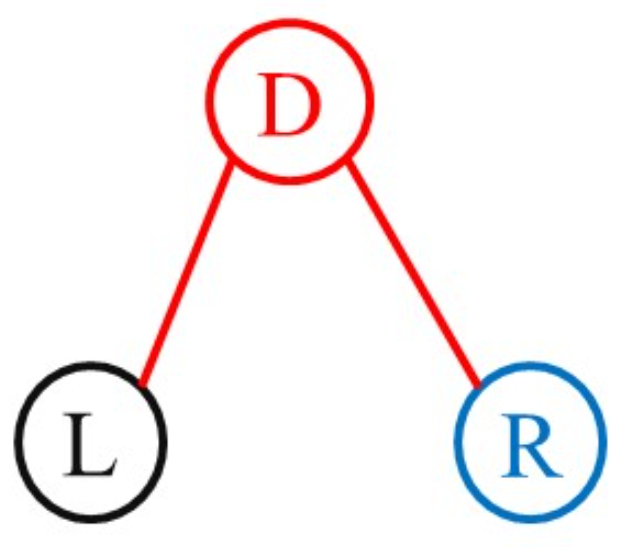
遍历规则:
- 前序遍历:D->L->R —> 根 左 右
- 中序遍历:L->D->R —> 左 根 右
- 后序遍历:L->R->D —> 左 右 根
- 层序遍历:从低到高逐层遍历
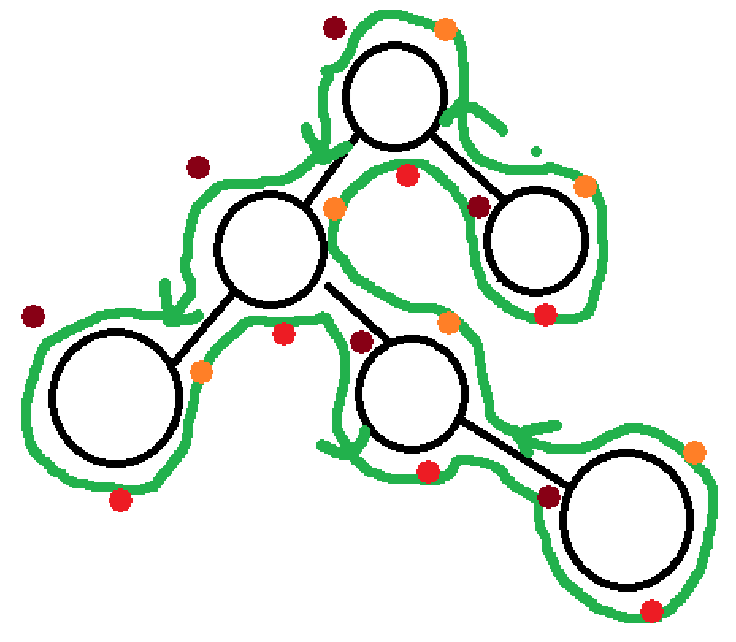
技巧:
- 对于前序,在左上方做标记
- 对于中序,在正下方做标记
- 对于后序,在右上方做标记
所有序列都逆时针遍历,根据标记可以得到遍历结果
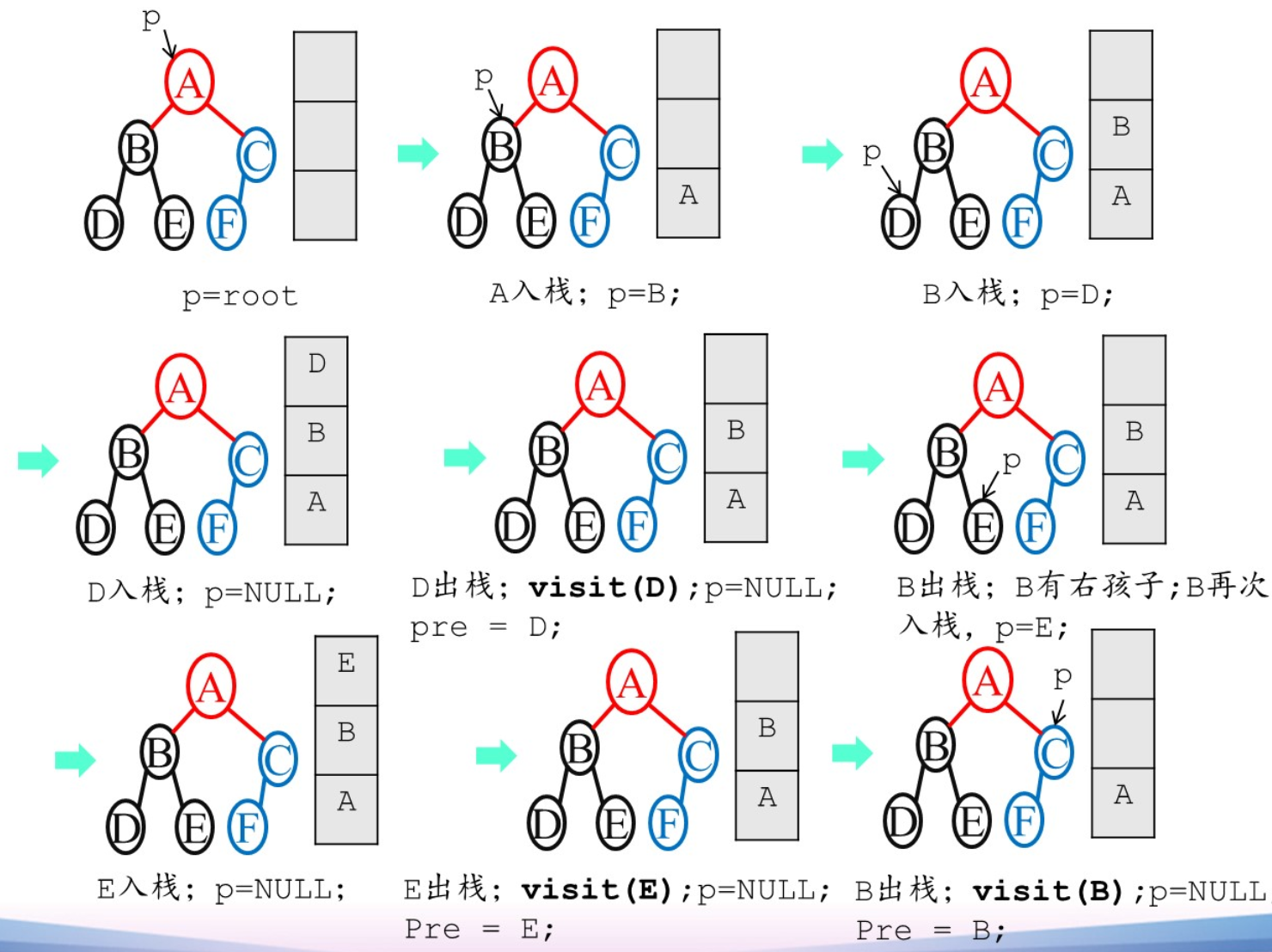
二叉树遍历的递归实现
递归工作栈最大深度和树的深度一致
- 最好情况,空间复杂度为$O(log_2n)$
- 最坏情况,空间复杂度为$O(n)$
前序遍历的代码实现:
- 入栈前访问
- 如果右孩子为空,则弹出栈顶元素(相当于回溯到父节点)Pop函数是弹出栈顶元素并赋值

中序遍历的代码实现:
- 出栈后访问

后序遍历的代码实现:
节点没有右孩子,或者右孩子刚被访问,则访问父节点
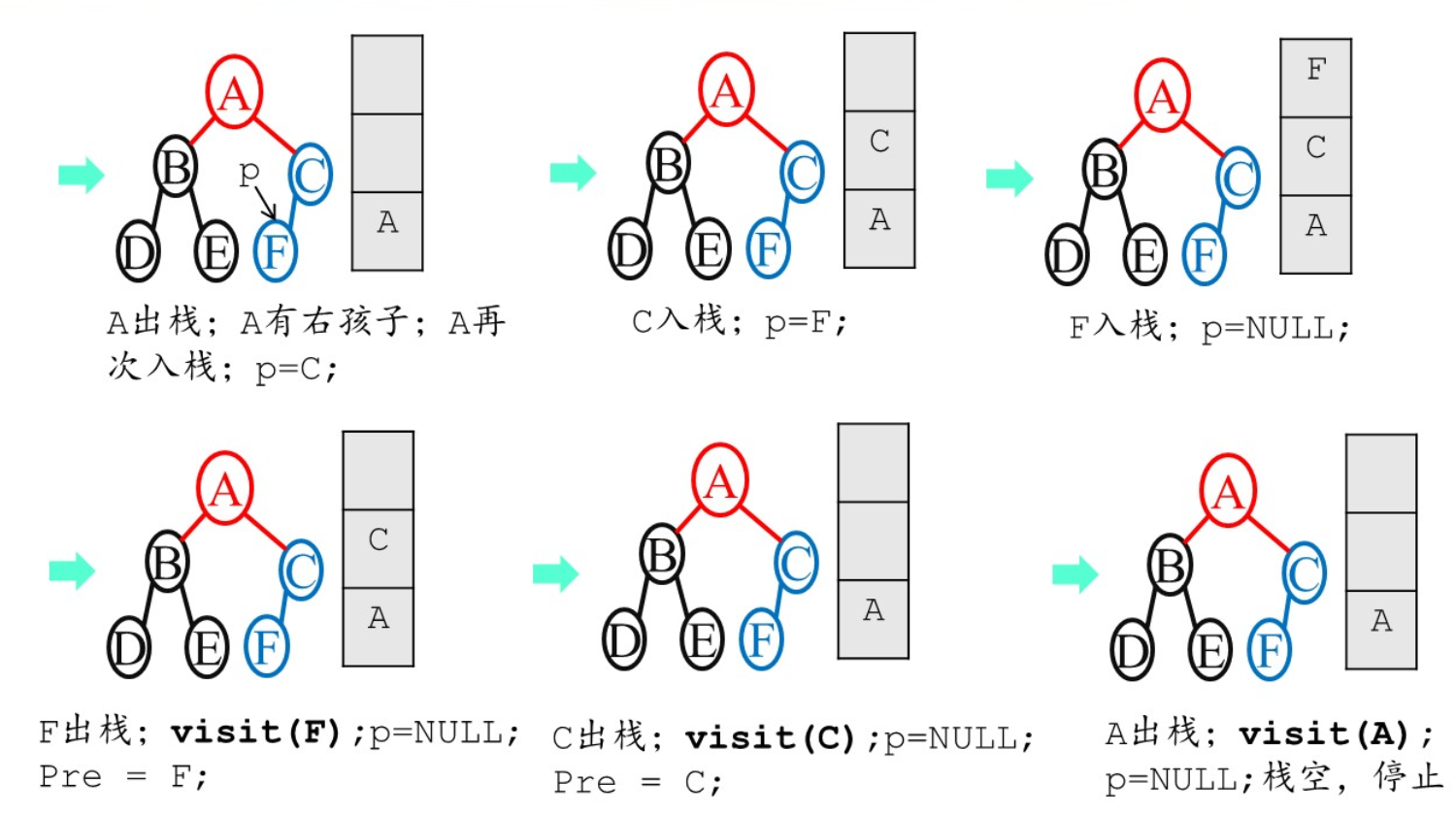
层序遍历的代码实现:
- 使用了队列去实现

重要结论:
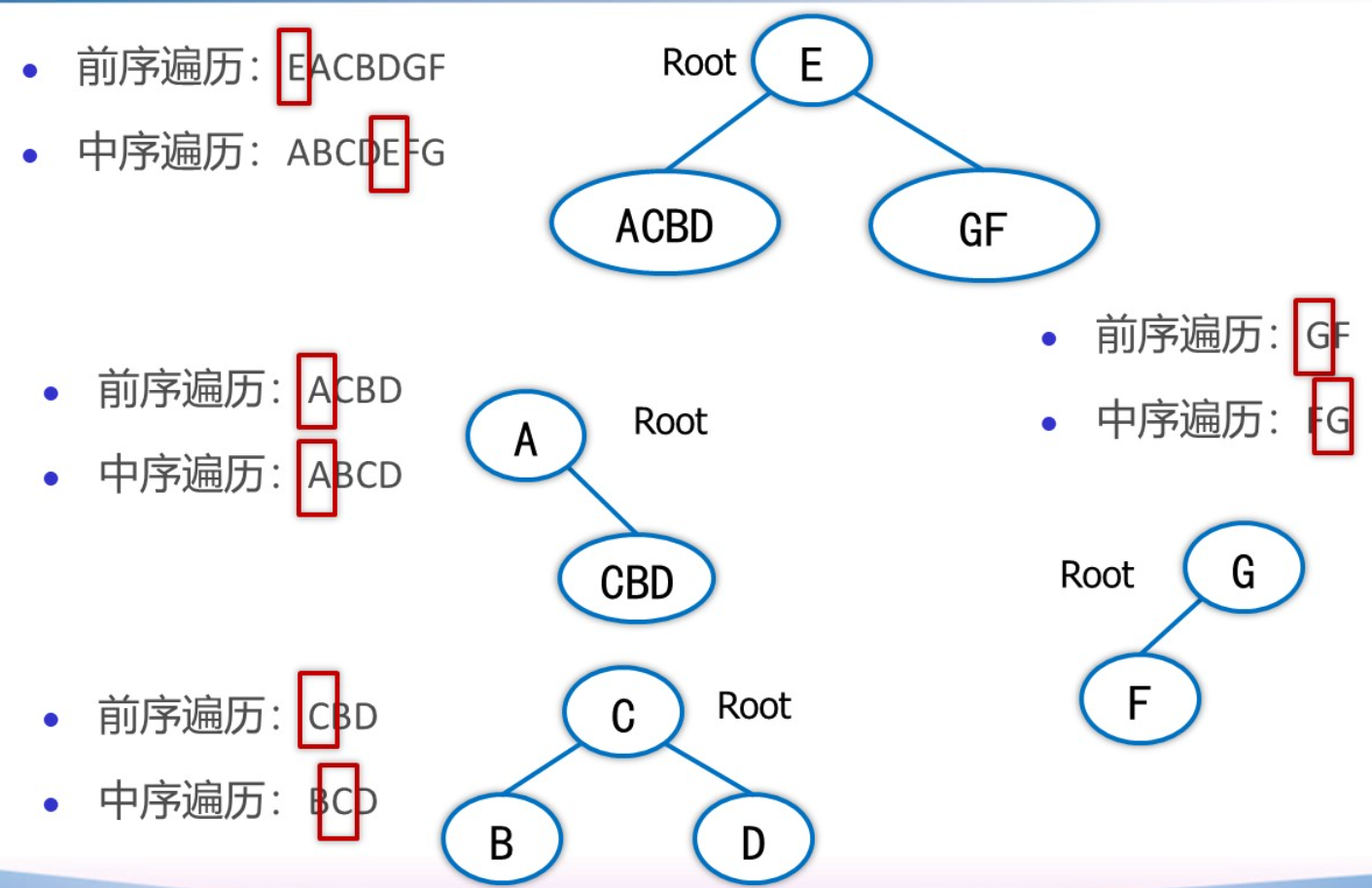
已知前序遍历序列和中序遍历序列,可以唯一确定一棵二又树。
已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
但是已知前序遍历序列和后序遍历序列,是不能确定一棵二又树的。
why?
前序遍历:第一个是根节点;后序遍历:最后一个是根节点
中序遍历:根节点在中间,左边是左子树右边是右子树
二叉树的应用
哈夫曼树
基本概念
伟大始于渺小
路径和路径长度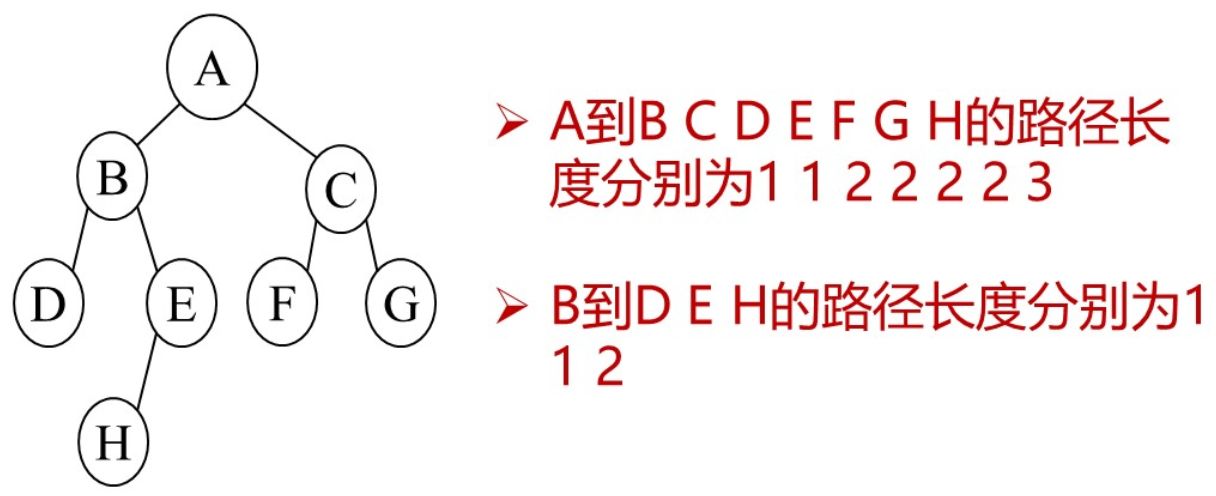
树的路径长度:从根到叶子节点的所有路径长度之和
节点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树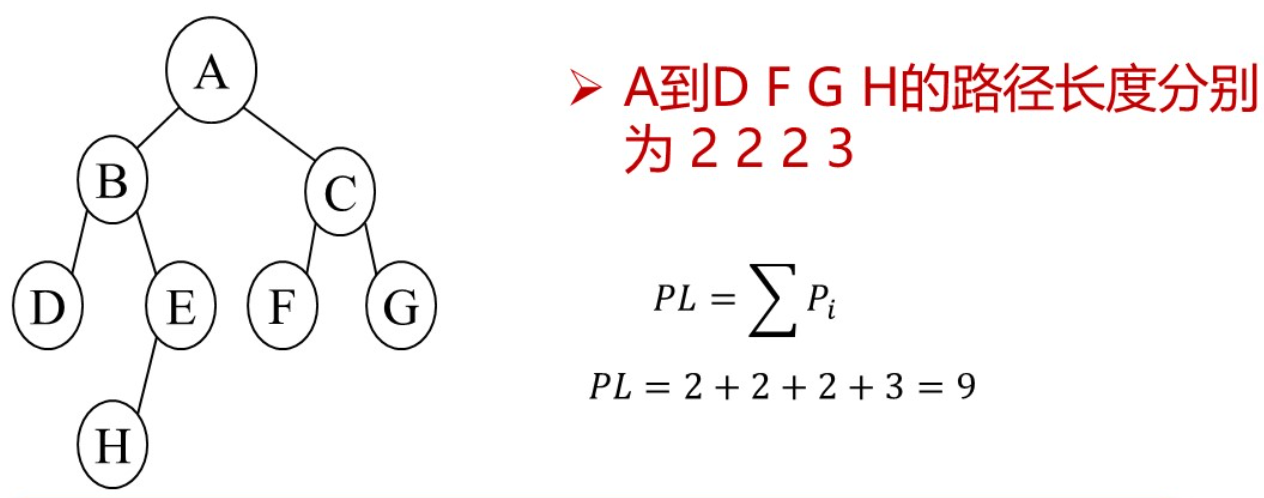
树的带权路径长度:所有根到叶子节点带权路径长度之和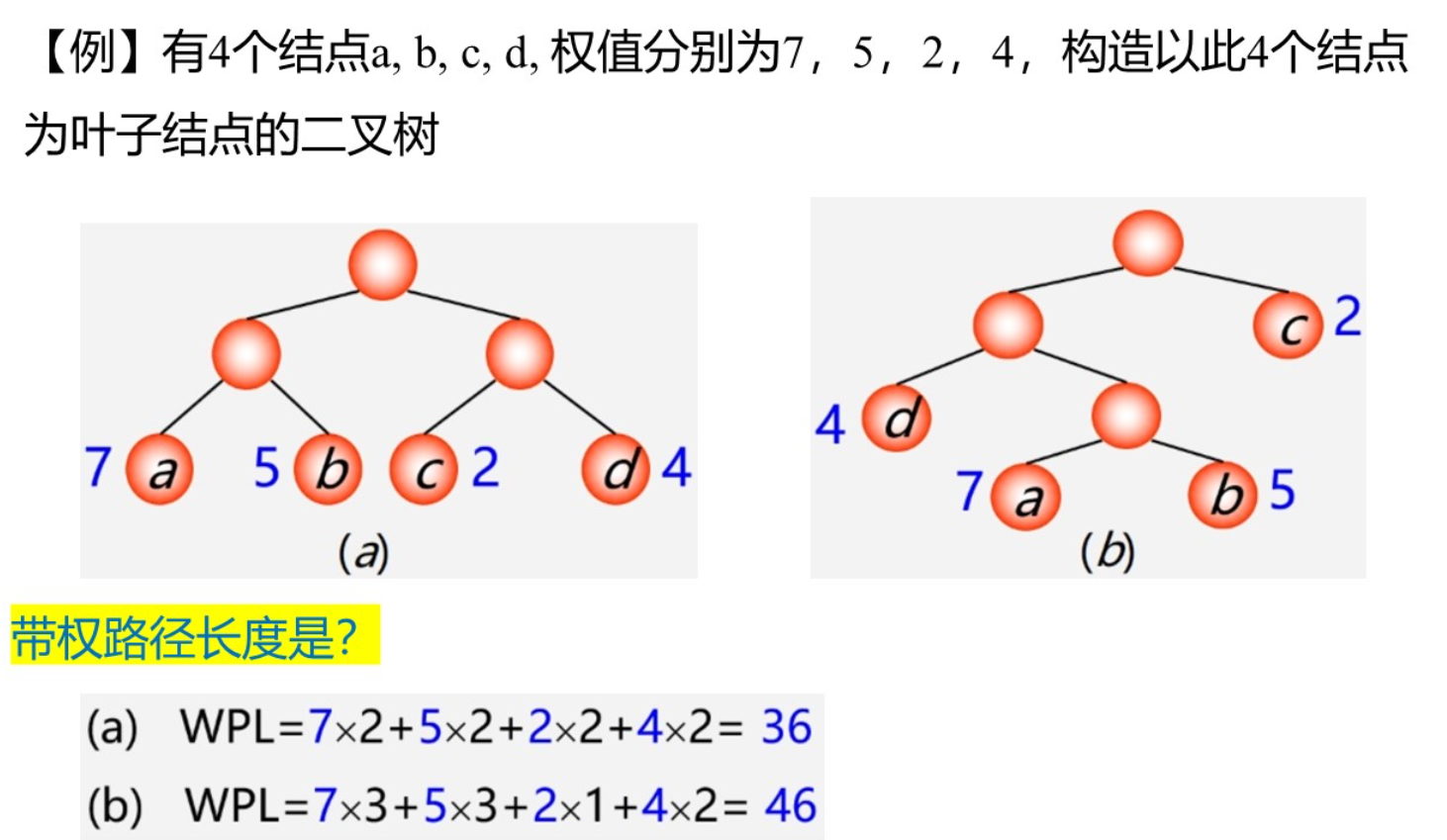
最优二叉树的构造
较为简单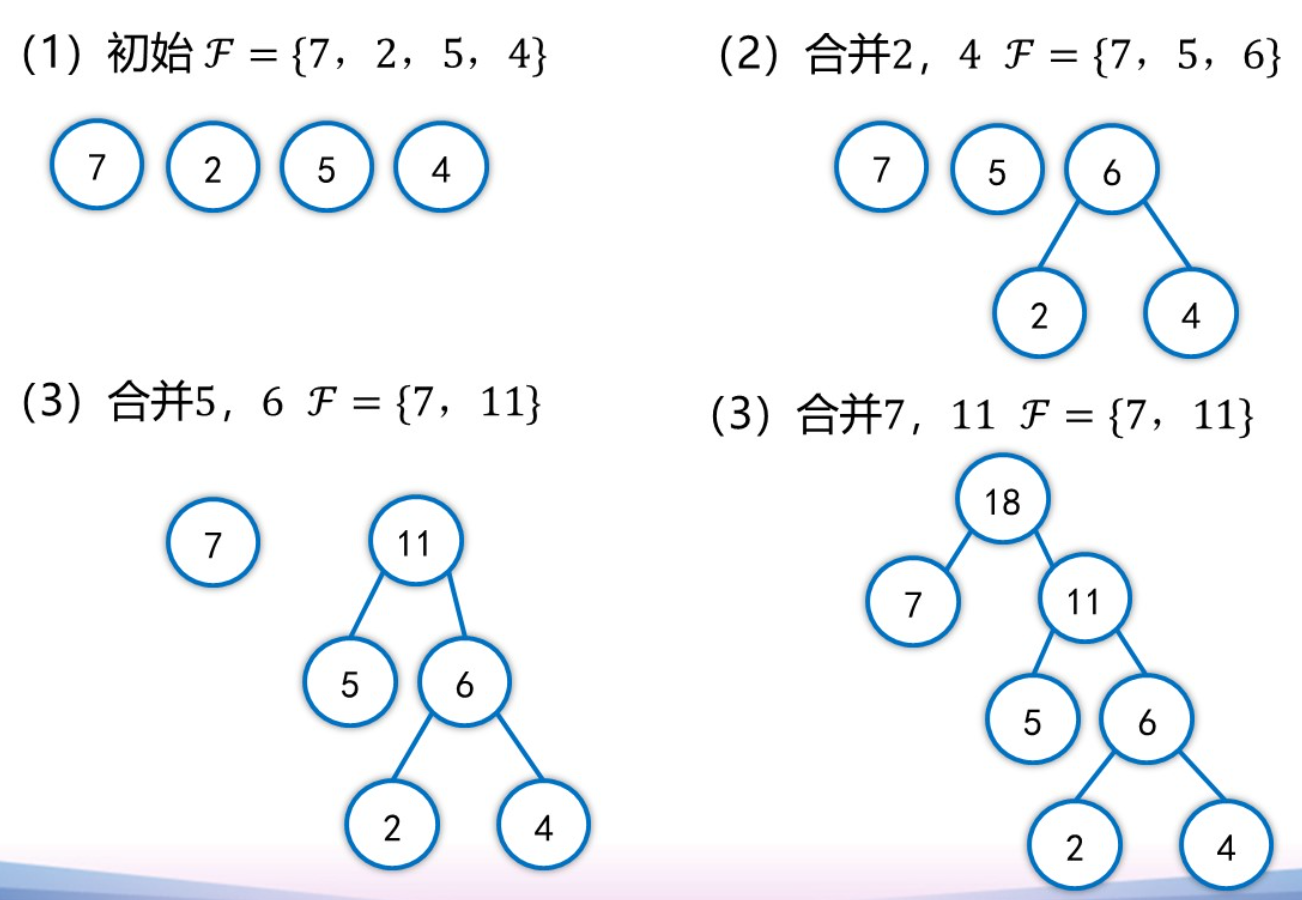
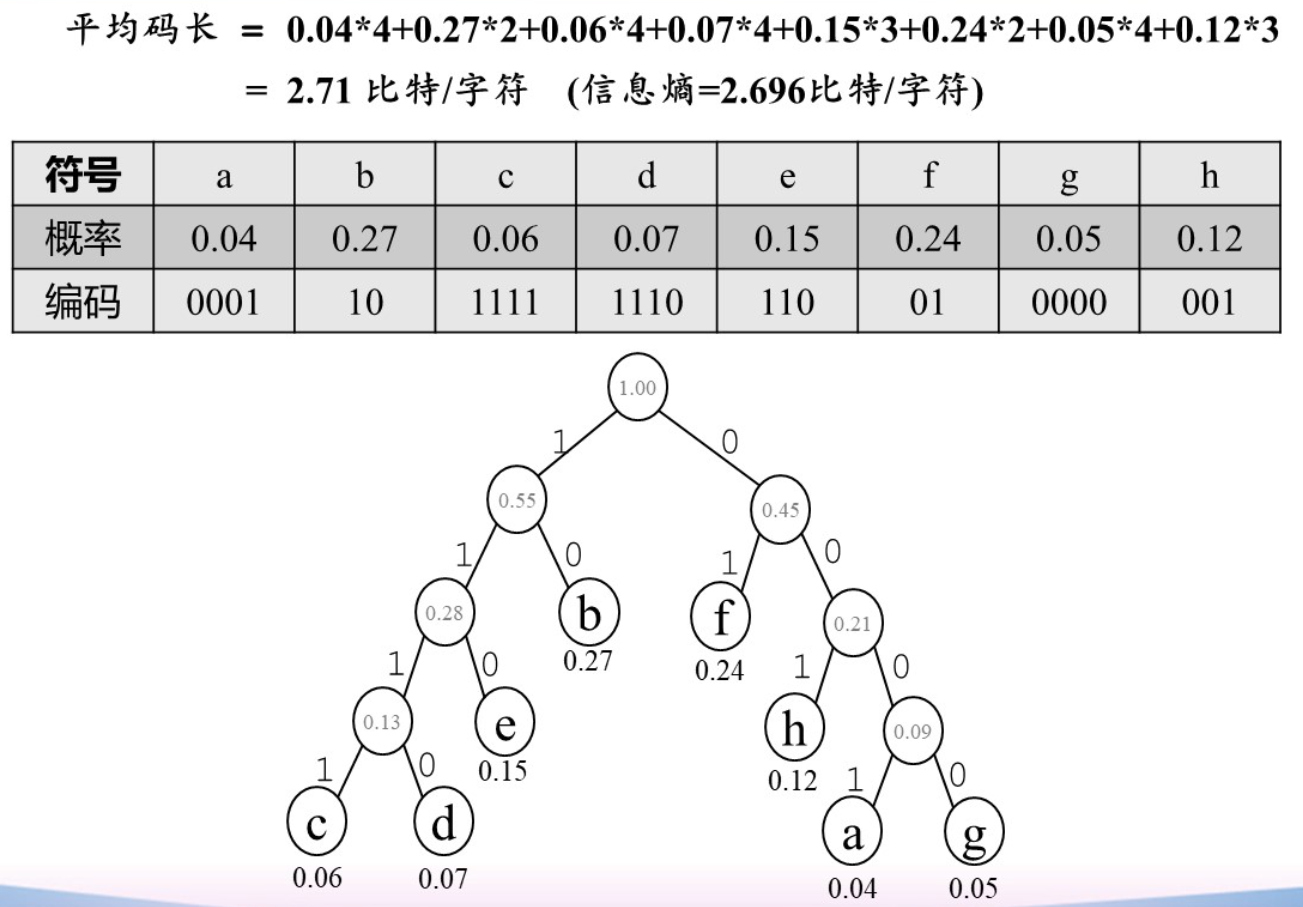
哈夫曼编码
优点:
- 概率大的路径短,概率小的路径长,使得树的带权路径长度短
- 任何字符编码都不是其他编码前缀,不会出现歧义
二叉搜索树
特点:
- 左子树小于根节点,右子树大于根节点
- 中序遍历二叉搜索树可以得到递增数列
- 查找的复杂度可能会从$O(log_2n)$退化为$O(n)$(不平衡的情况)
中序遍历结果相同的二叉搜索树不唯一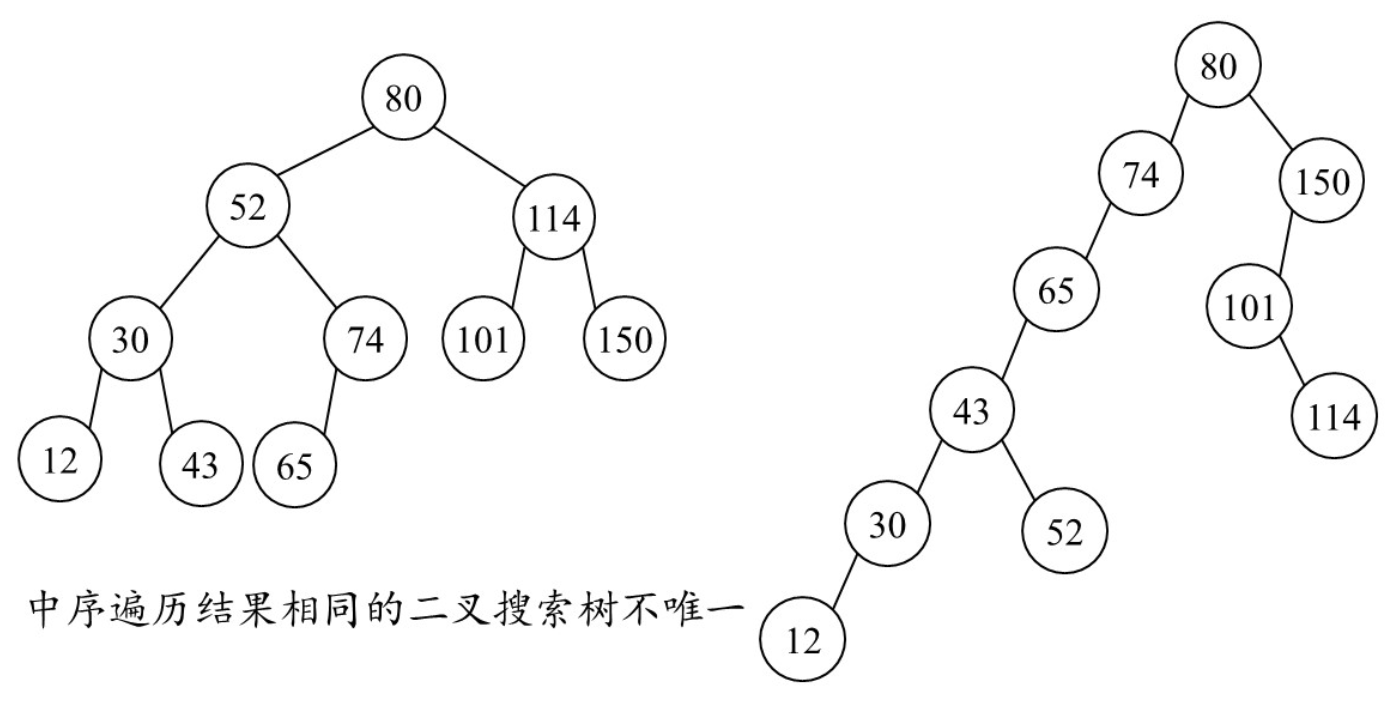
二叉搜索树的删除
用节点的中序遍历的前驱/后继代替
e.g.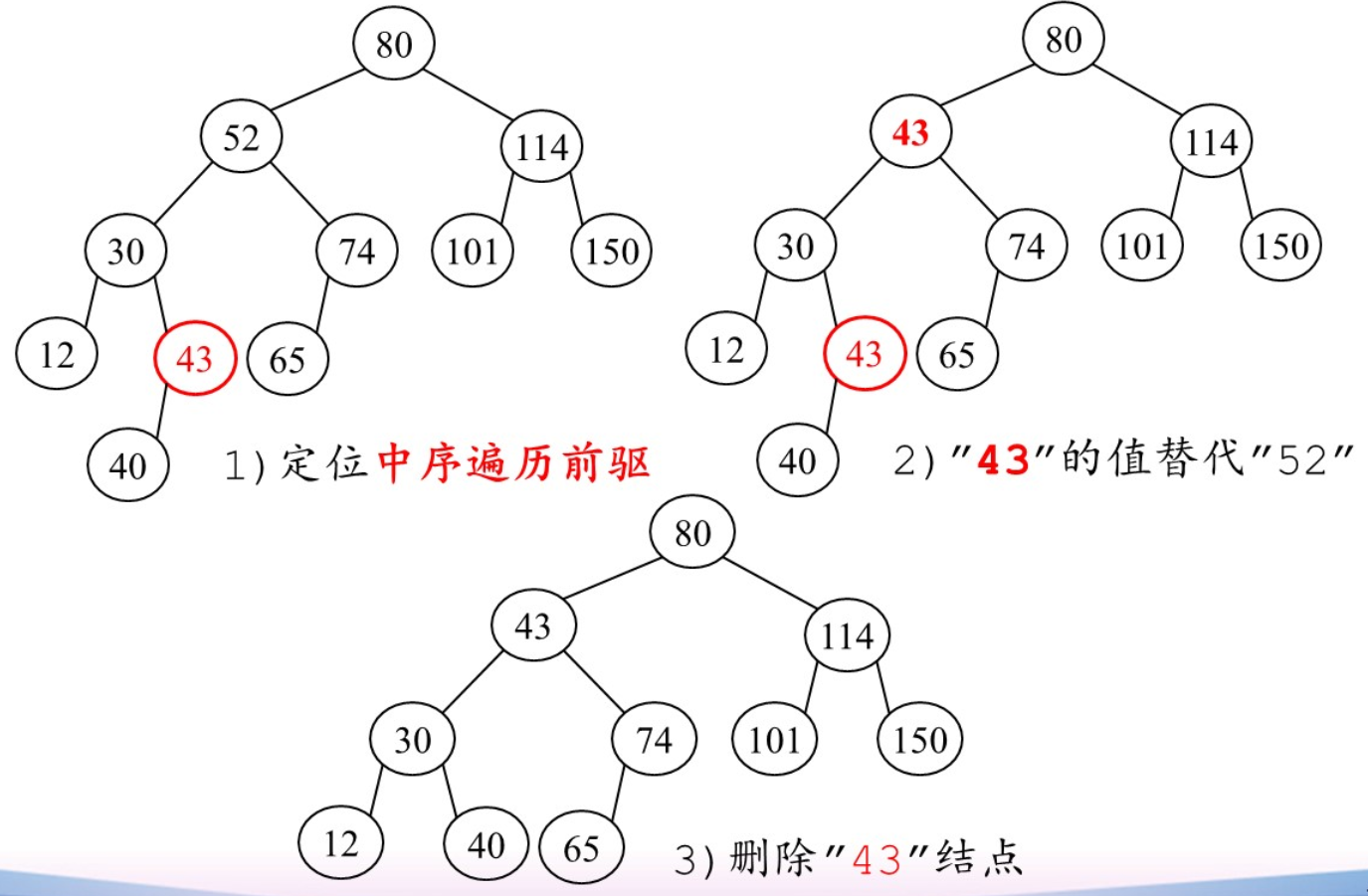
AVL树
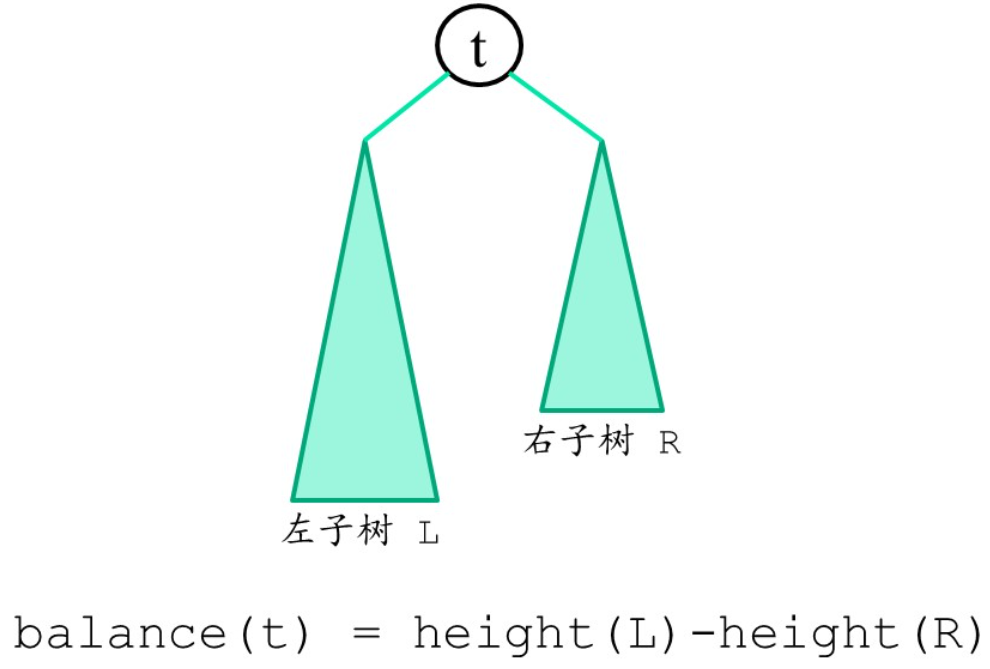
特点:
旋转操作
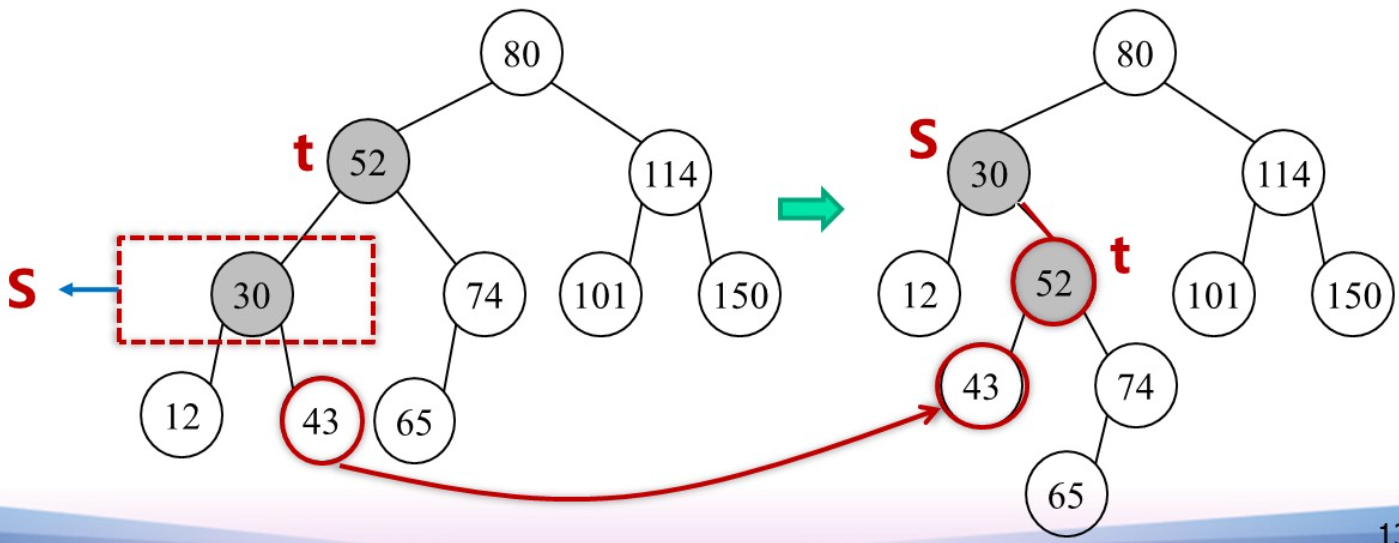
右旋转
代码实现:
步骤:
- 根节点的父亲指向子节点
- 子节点的右孩子成为根节点的左孩子
- “交换父子关系”:根节点成为子节点的右孩子
左旋转
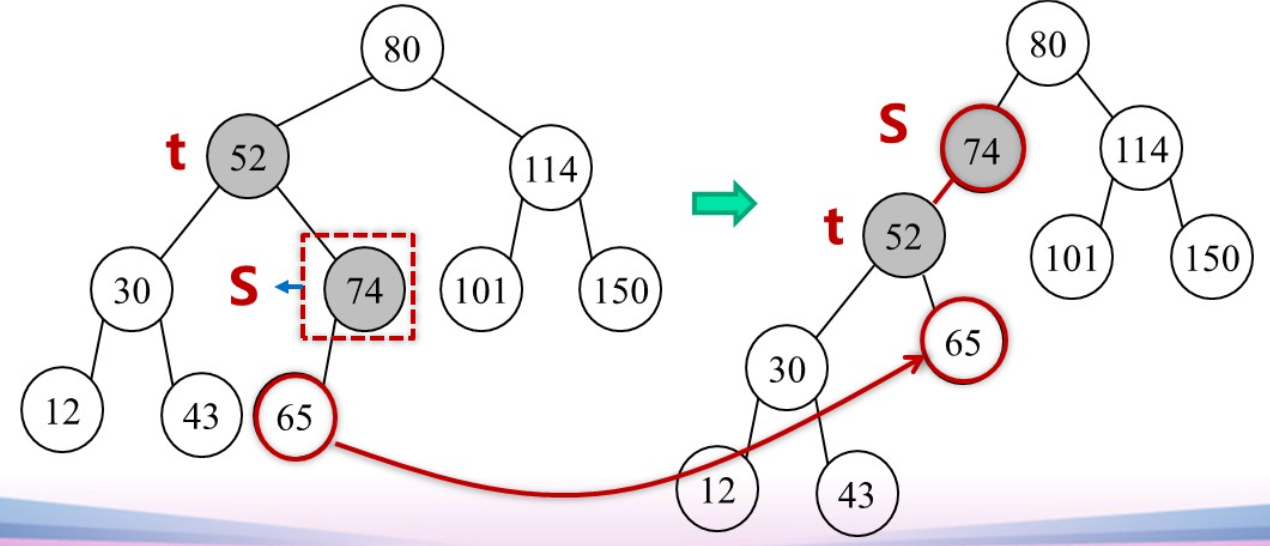
代码实现: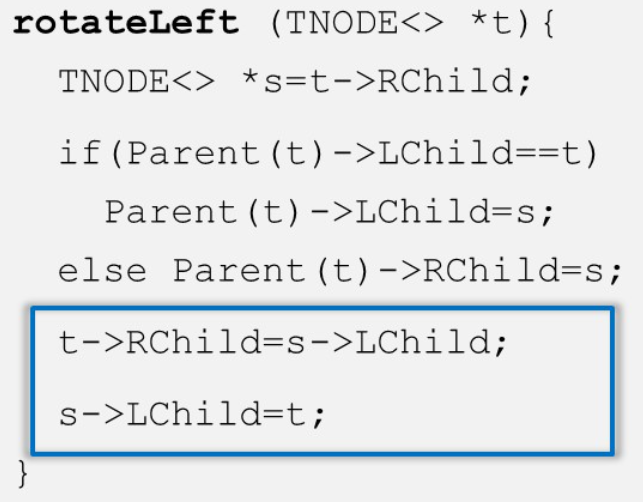
步骤:
- 根节点的父亲指向子节点
- 子节点的左孩子成为根节点的右孩子
- “交换父子关系”:根节点成为子节点的左孩子
节点插入
节点插入会破坏树的平衡性,需要进行旋转达到平衡
插入“18”,根节点的平衡因子变为2,因此需要进行旋转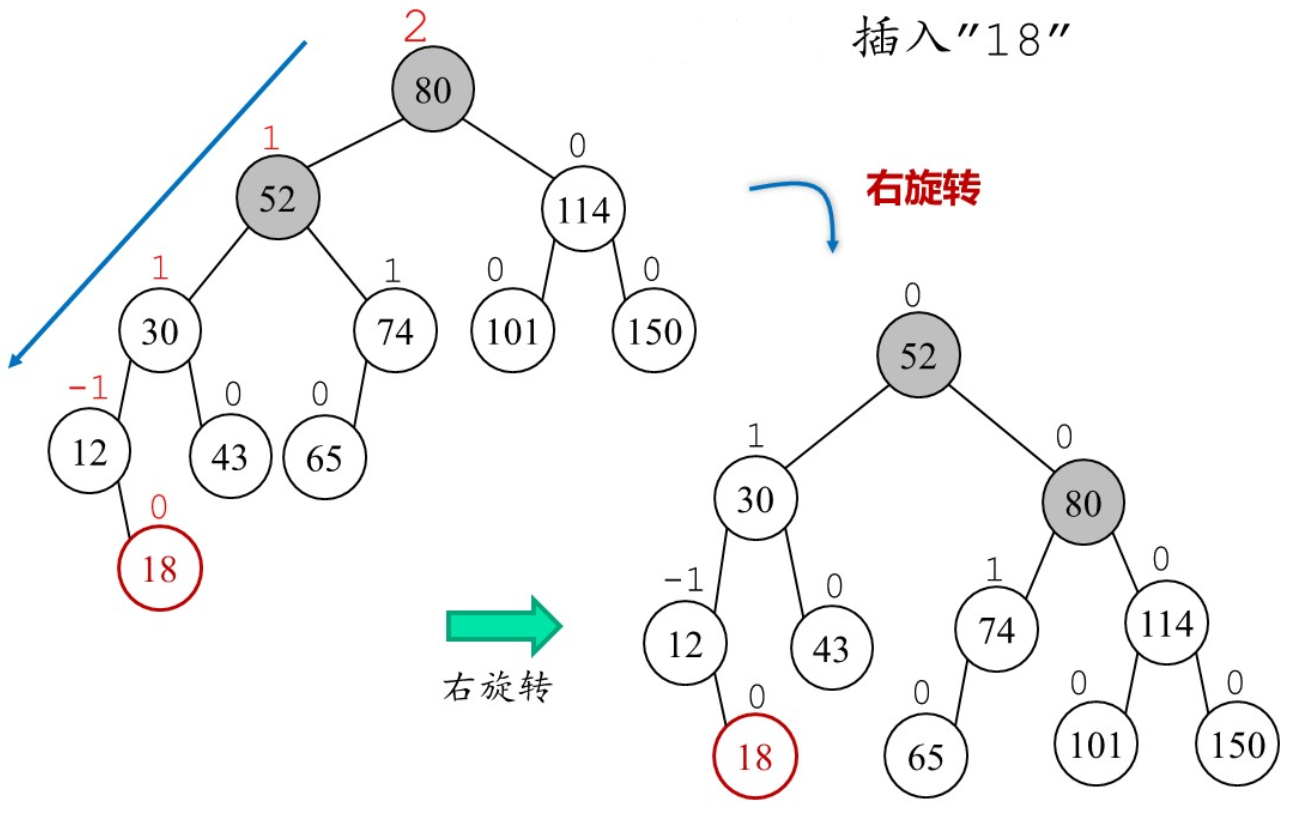
不能随意旋转,最终还是要看是否所有平衡因子达到要求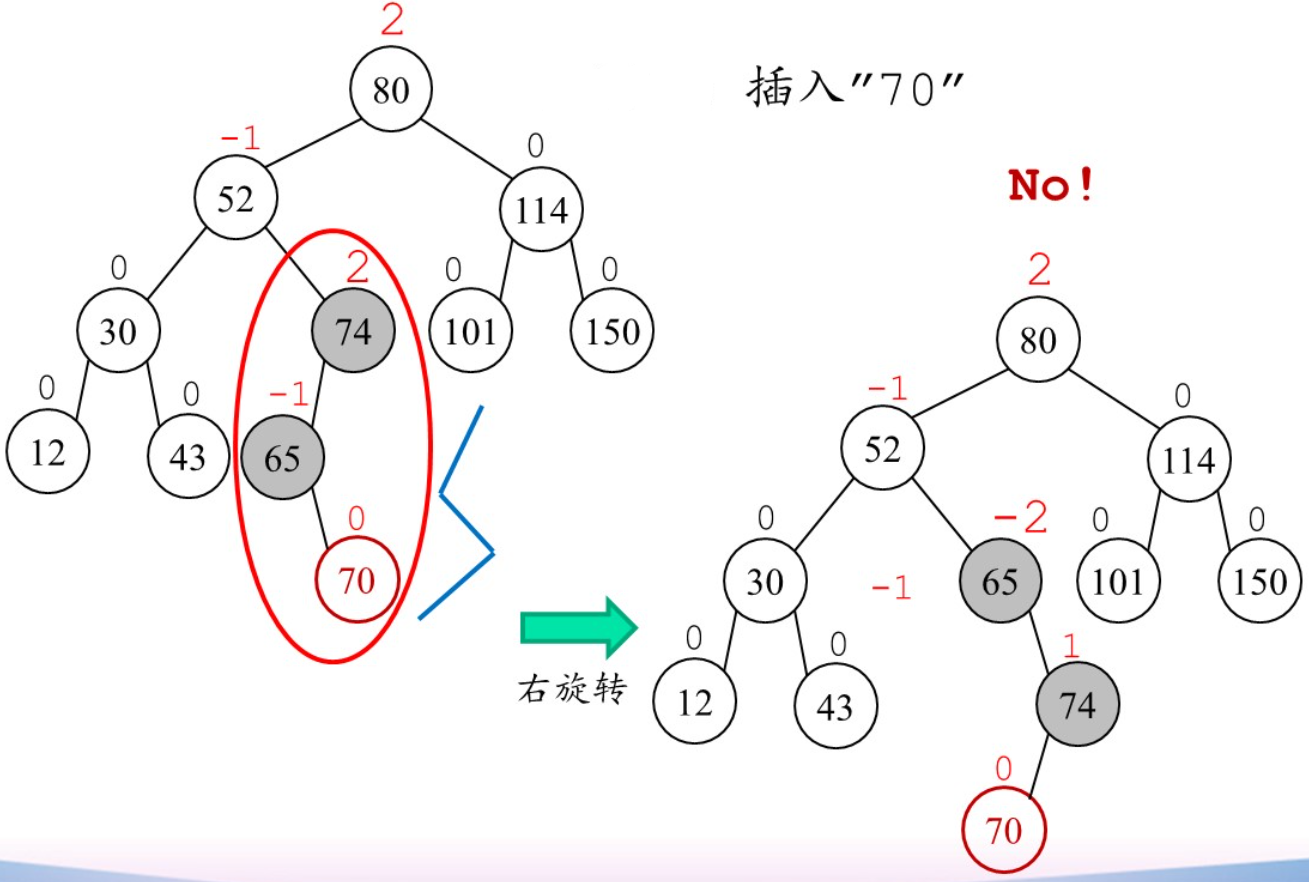
可进行多次旋转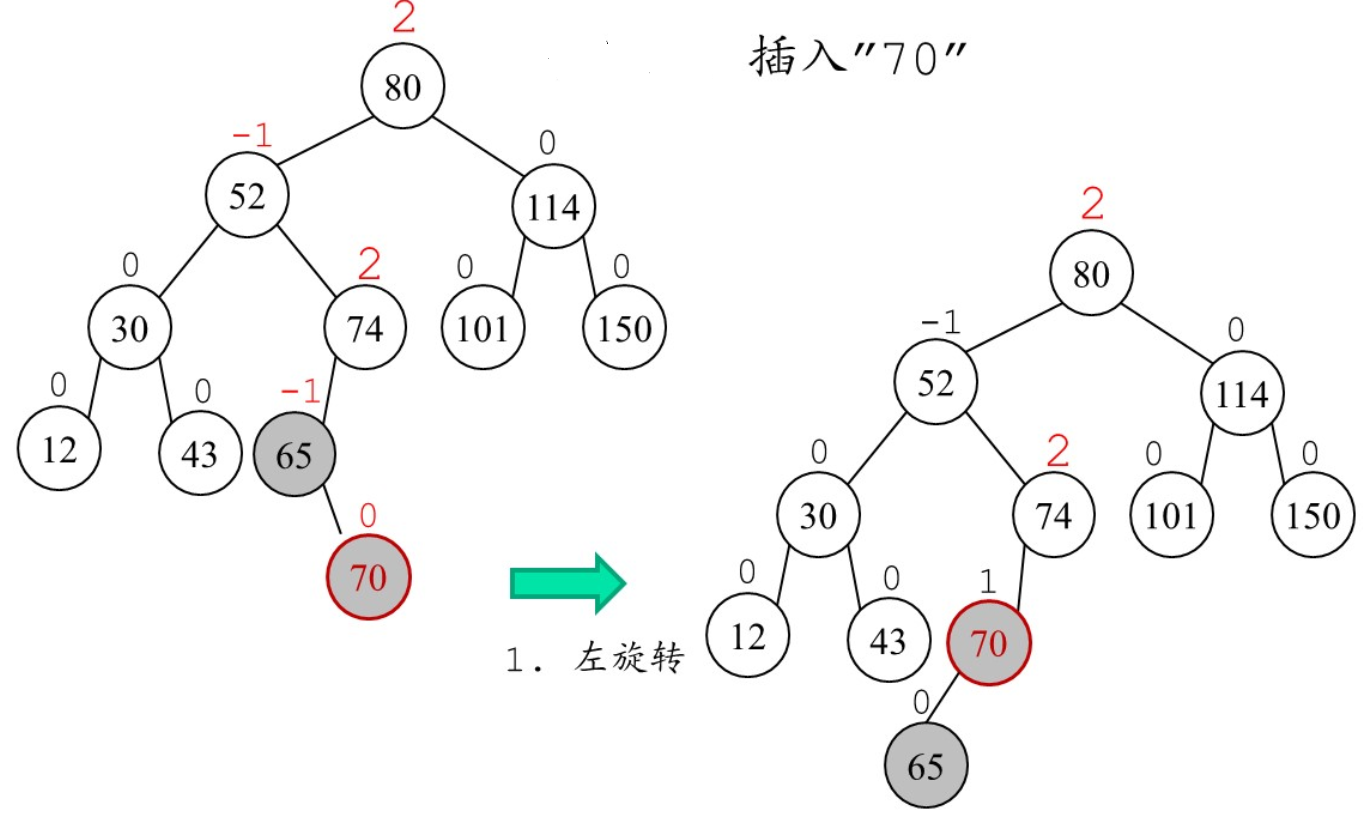
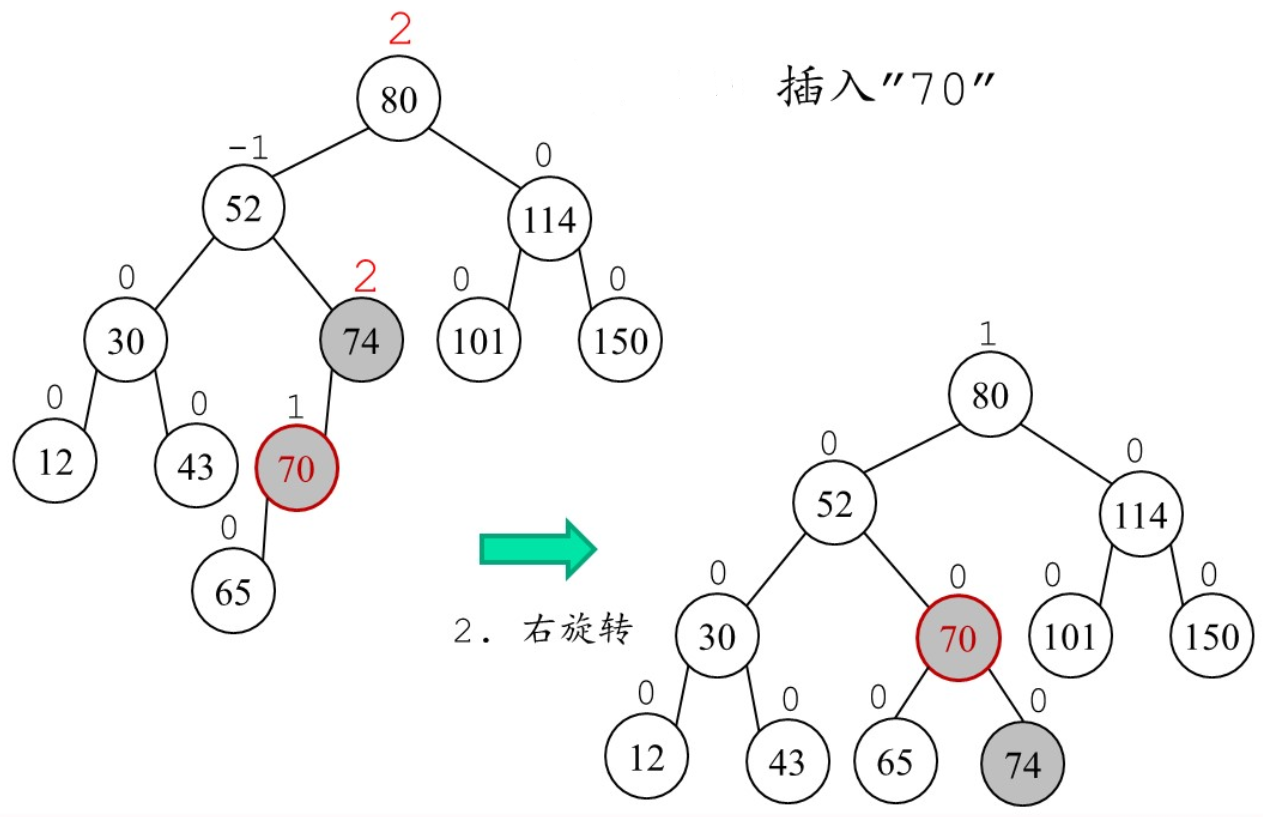
红黑树
特点:
- 一种“自平衡”的二叉查找树,可以应对极端情况O(N)
- 复杂度介于 $O(log_2N)$和$O(N)$
- 是一种接近平衡的二叉树
红黑树保证最长路径不超过最短路径的二倍,因而近似平衡(最短路径就是全黑节点,最长路径就是一个红节点一个黑节点,当从根节点到叶子节点的路径上黑色节点相同时,最长路径刚好是最短路径的两倍)。它同时满足以下特性:
- 节点是红色或黑色
- 根是黑色
- 叶子节点(外部节点,空节点)都是黑色,这里的叶子节点指的是最底层的空节点(外部节点),下图中的那些null节点才是叶子节点,null节点的父节点在红黑树里不将其看作叶子节点
- 红色节点的子节点都是黑色;红色节点的父节点都是黑色;从根节点到叶子节点的所有路径上不能有 2 个连续的红色节点
- 从任一节点到叶子节点的所有路径都包含相同数目的黑色节点
e.g.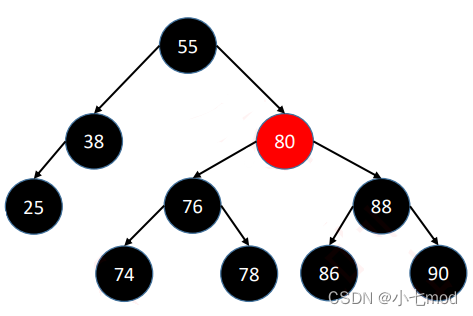
上面这棵树首先很容易就能知道是满足性质1-4条的,关键在于第5条性质,可能乍一看好像也是符合第5条的,但实际就会陷入一个误区,直接将图上的最后一层的节点看作叶子节点,这样看的话每一条从根节点到叶子结点的路径确实都经过了3个黑节点。
但实际上,在红黑树中真正被定义为叶子结点的,是那些空节点,如下图。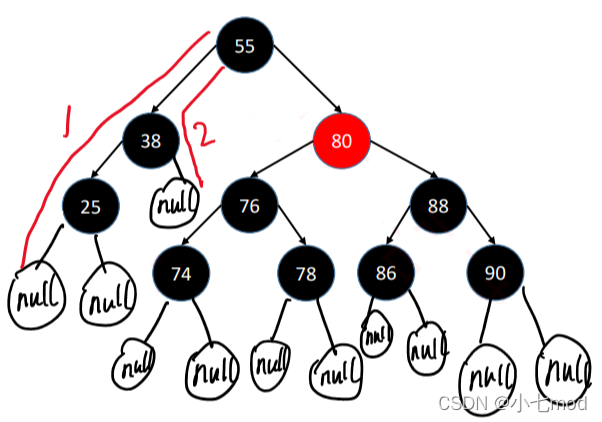
这样一来,路径1有4个黑色节点(算上空节点),路径2只有3个黑色节点,这样性质5就不满足了,所以这棵树并不是一个红黑树节点。
效率
红黑树的查找,插入和删除操作,时间复杂度都是$O(logN)$。
查找操作时,它和普通的相对平衡的二叉搜索树的效率相同,都是通过相同的方式来查找的,没有用到红黑树特有的特性。
但如果插入的时候是有序数据,那么红黑树的查询效率就比二叉搜索树要高了,因为此时二叉搜索树不是平衡树,它的时间复杂度$O(N)$。
插入和删除操作时,由于红黑树的每次操作平均要旋转一次和变换颜色,所以它比普通的二叉搜索树效率要低一点,不过时间复杂度仍然是$O(logN)$。总之,红黑树的优点就是对有序数据的查询操作不会慢到$O(logN)$的时间复杂度。
与AVL树的比较
- AVL树的时间复杂度虽然优于红黑树,但是对于现在的计算机,cpu太快,可以忽略性能差异
- 红黑树的插入和删除操作比AVL树更便于控制操作
- 红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)
- 对于AVL树来说,搜索、添加、删除都是 $O(logn)$ 复杂度,其中添加仅需 $O(1)$ 次旋转调整、删除最多需要 $O(logn)$ 次旋转调整
- 对于红黑树来说,搜索、添加、删除都是 $O(logn)$ 复杂度,其中添加、删除都仅需 $O(1)$ 次旋转调整
- AVL树通过严格的平衡条件确保树的高度始终接近理论下限。这使得搜索操作更快,因为路径更短。
- 红黑树通过颜色标记和宽松的平衡规则(如根到叶子的最长路径不超过最短路径的两倍)。虽然搜索效率略低于AVL树,但插入和删除操作更高效
如何选择?
- 搜索的次数远远大于插入和删除,选择AVL树;搜索、插入、删除次数几乎差不多,选择红黑树
- 相对于AVL树来说,红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树
- 红黑树的平均统计性能优于AVL树,实际应用中更多选择使用红黑树