图
图
图的基本概念
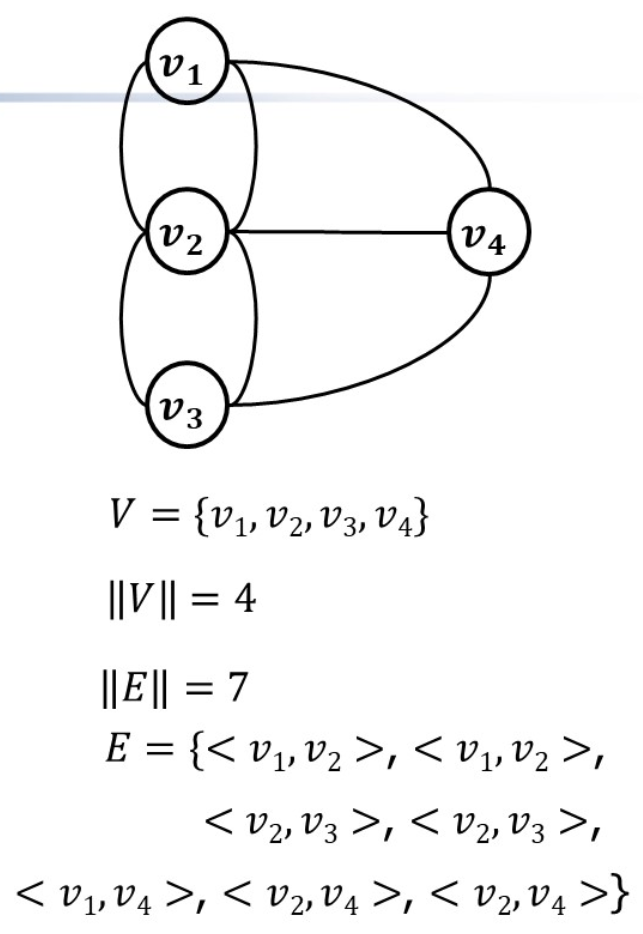
顶点集、边集、顶点数目、边数目
有向图和无向图的区别
有向图的边集$\mathbf{E}$中的元素有序而无向图的边集$\mathbf{E’}$中的元素无序
简单图
不存在自环和多重边(两条边的起点和终点相同)
这里讨论的都是简单图
无向完全图和有向完全图的区别
完全图:图中的每个顶点和其余顶点都有边相连
无向完全图的边数:$e = n (n - 1) / 2$
有向完全图的边数:$e = n (n - 1)$
拥有$n$个顶点的无向图一共有$2 ^ {n (n - 1) / 2}$种
拥有$n$个顶点的有向图一共有$2 ^ {n (n - 1)}$种
为什么?
有向图和无向图最多可能有的边数就是他们成为完全图的边数
子图和超图

每个图都是自身的子图,空图是任何图的子图
拥有$n$个顶点的图一定是这$n$个顶点组成的完全图的子图
顶点的度
顶点的度记作$TD(v)$,入度记作$ID(v)$,出度记作$OD(v)$
有:$ TD(v) = ID(v) + OD(v) $
度为奇数的顶点成为奇点,度为偶数的顶点称为偶点
重要性质:
有向图中所有顶点入度之和等于所有顶点出度之和(每条边贡献一个入度和一个出度)握手定理:
图中所有顶点度之和等于边数目的2倍(每条边贡献两个度)推论一:
有向图中所有顶点入度或出度之和等于边数目
推论二:
任意图中一定有偶数个(含0)奇点对于树来说:
- 边数等于度数之和
- 边数等于节点数减一
路径和回路
没有重复节点,则成为简单路径/回路
连通图
无向图中$G$,如果任意两个顶点都是连通的,则$G$是连通图;有向图$G$中,如果任意两个顶点都存在路径,则$G$是强连通图
极大连通子图(连通分量):该图是$G$的连通子图,将$G$中任何不在该子图中的顶点加入,子图将不再连通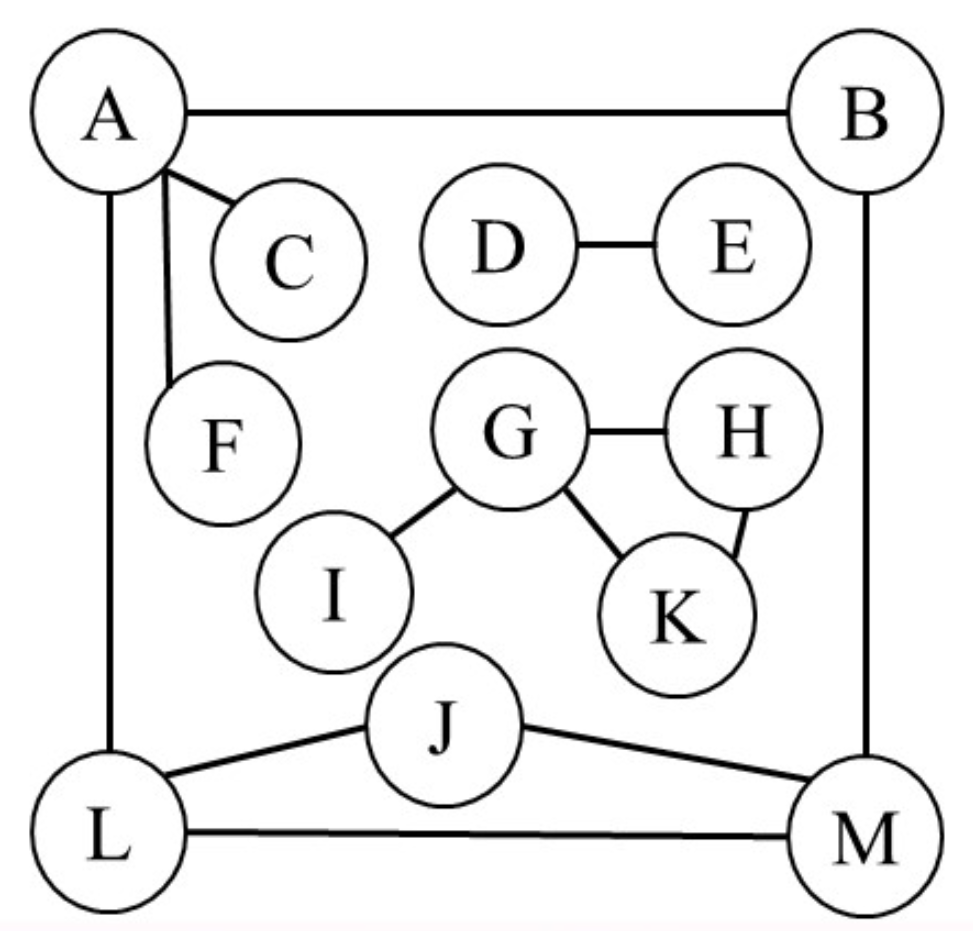
补图
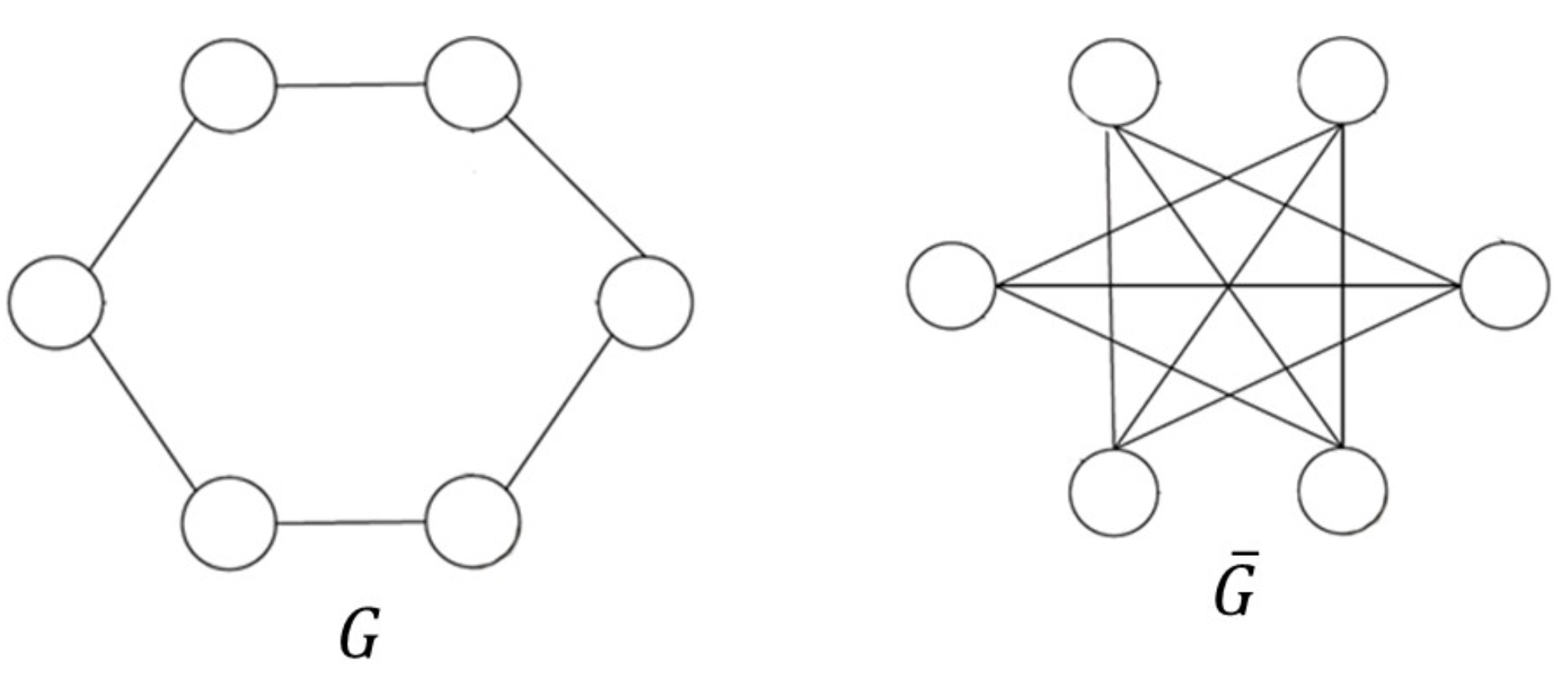
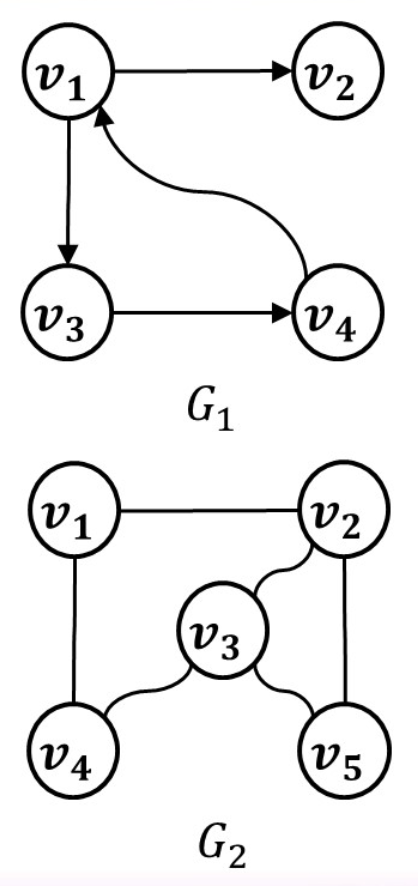
同构
形变过后得到的图
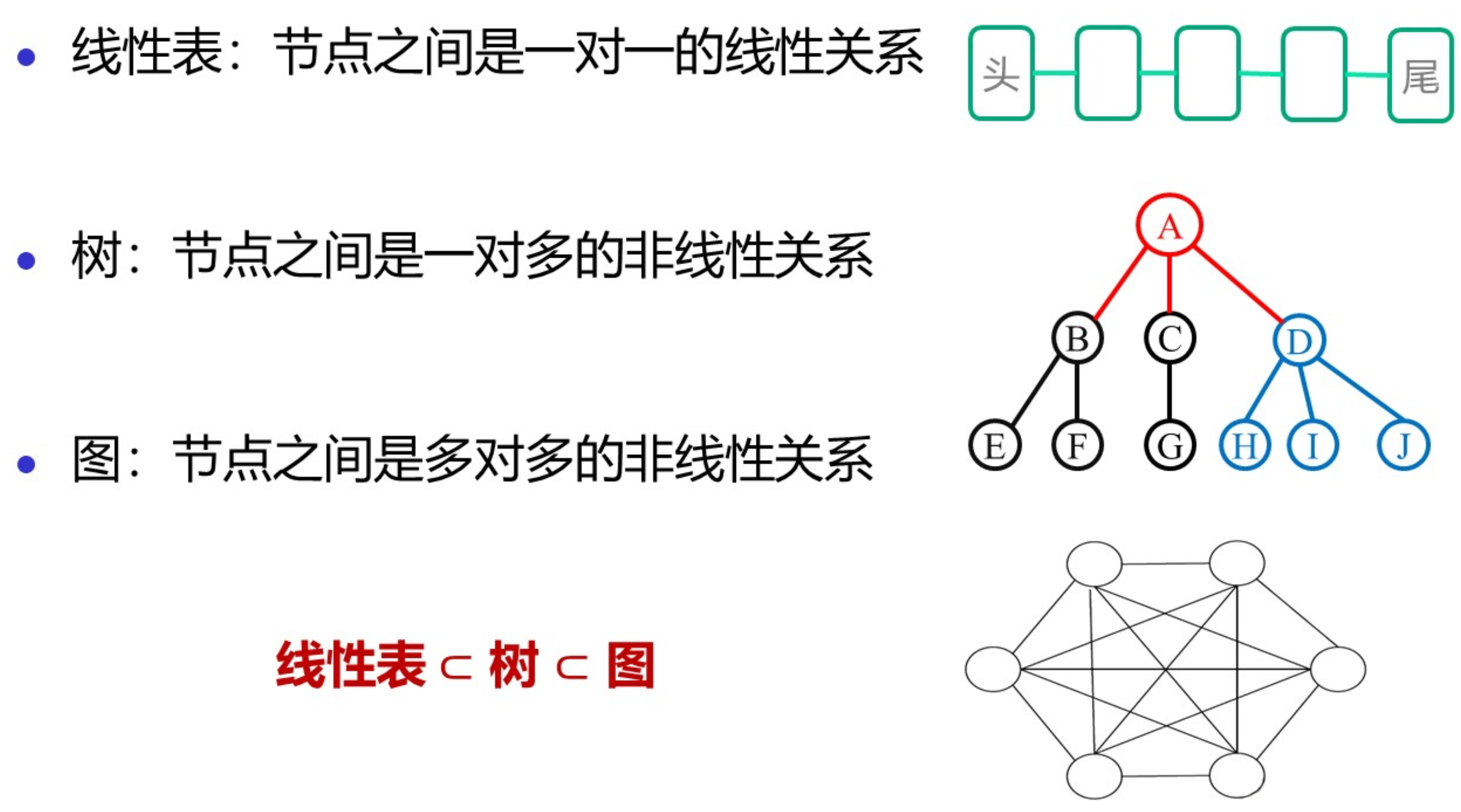
线性表、树、图的比较
欧拉路径和回路
欧拉路径:图中经过每条边且仅经过每条边一次的路径
欧拉回路:终点和起点重合的欧拉路径
定理:
图的存储结构
通常采用两个数组来表示一个图
其一用来存储顶点信息;其二用来存储顶点的关联情况,称为邻接矩阵
顶点信息:
邻接矩阵: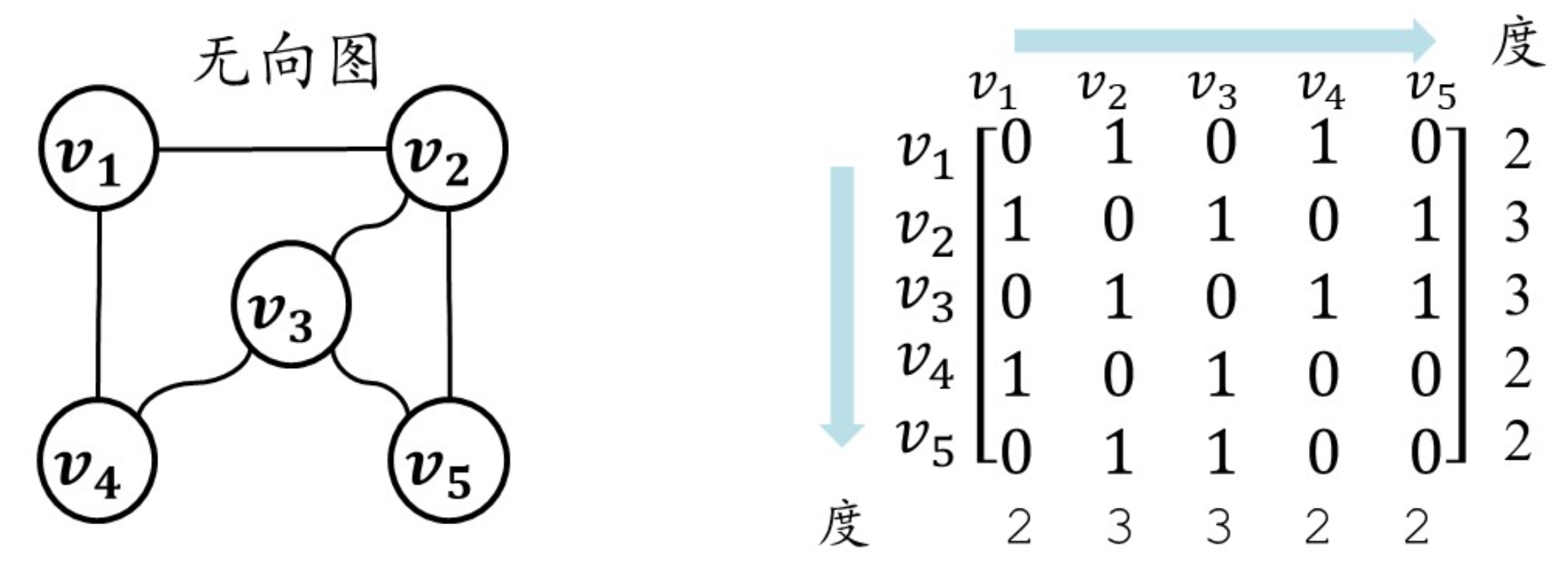
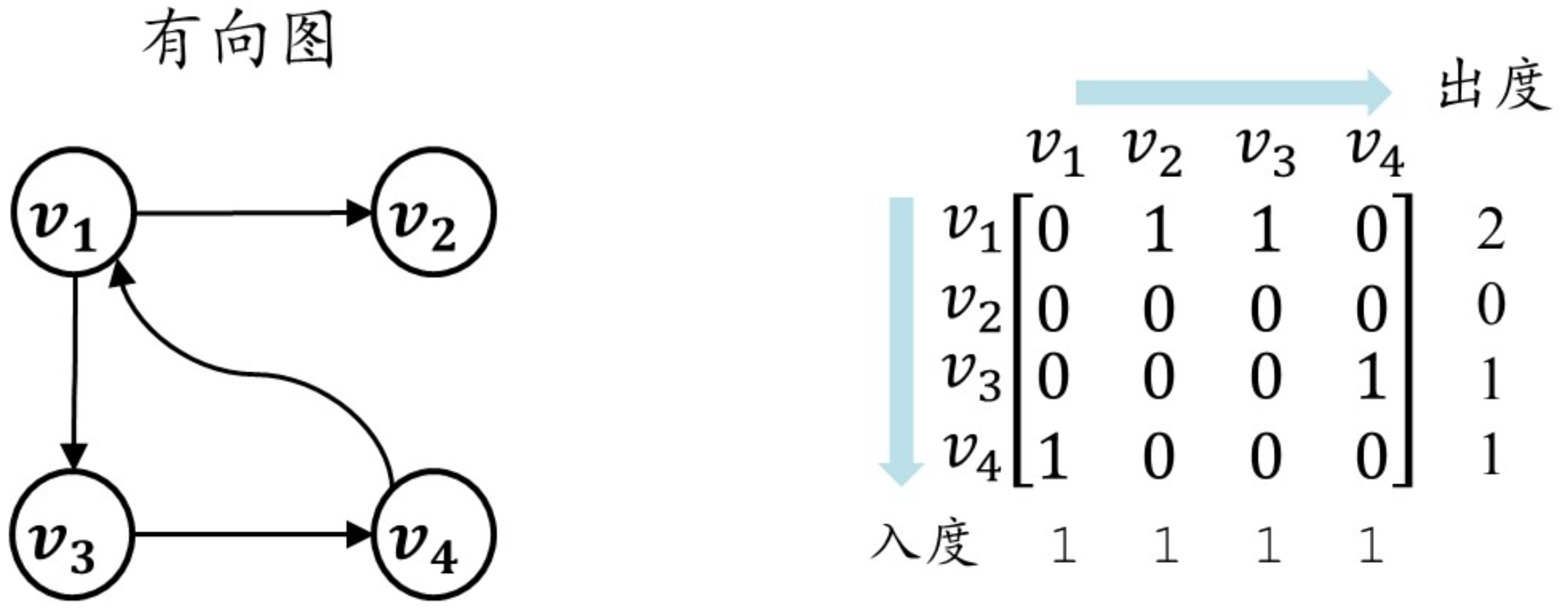
重要特点:无向图的邻接矩阵对称,有向图则不一定
邻接矩阵实现

为什么添加/删除顶点的时间复杂度是$O(n^2)$?
邻接矩阵通过 n×n 的二维数组 存储顶点间的边关系。当添加一个新顶点时:
需要将原矩阵从 n×n 扩容到 (n+1)×(n+1),即创建一个新的二维数组。复制原有 n×n 数据到新数组,并初始化新增行/列(通常用 0 填充表示无边)。这一过程中,复制原有数据需要遍历所有 n² 个元素,因此时间复杂度为 O(n²)。
邻接表
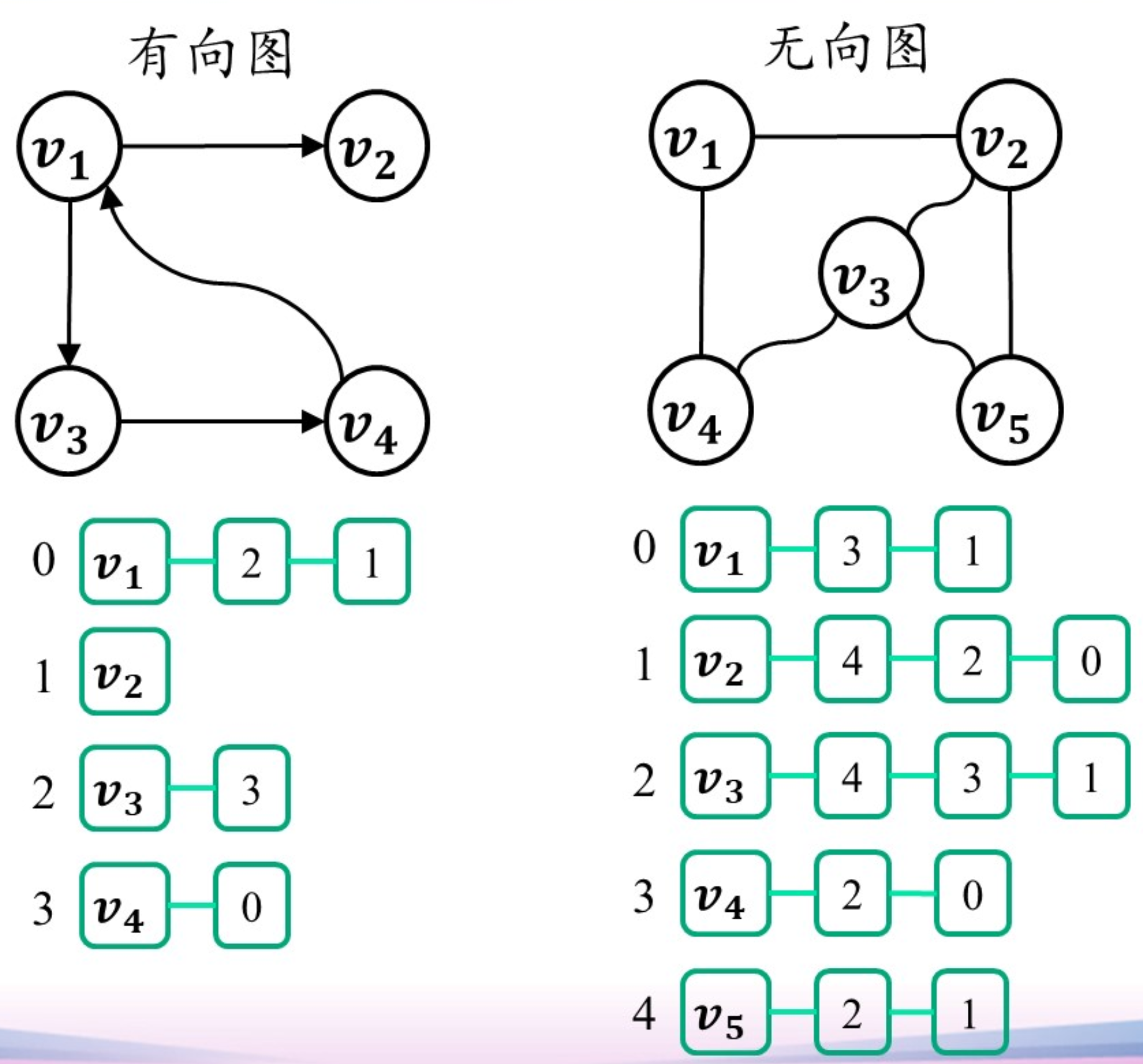
有向图每个链表的长度等于顶点的出度,总共需要$(n + e)$个链表结点
无向图每个链表的长度等于顶点的度,总共需要$(n + 2e)$个链表结点
邻接表的实现:
注意插入边和删除边的时间复杂度不同
邻接矩阵和邻接表的比较
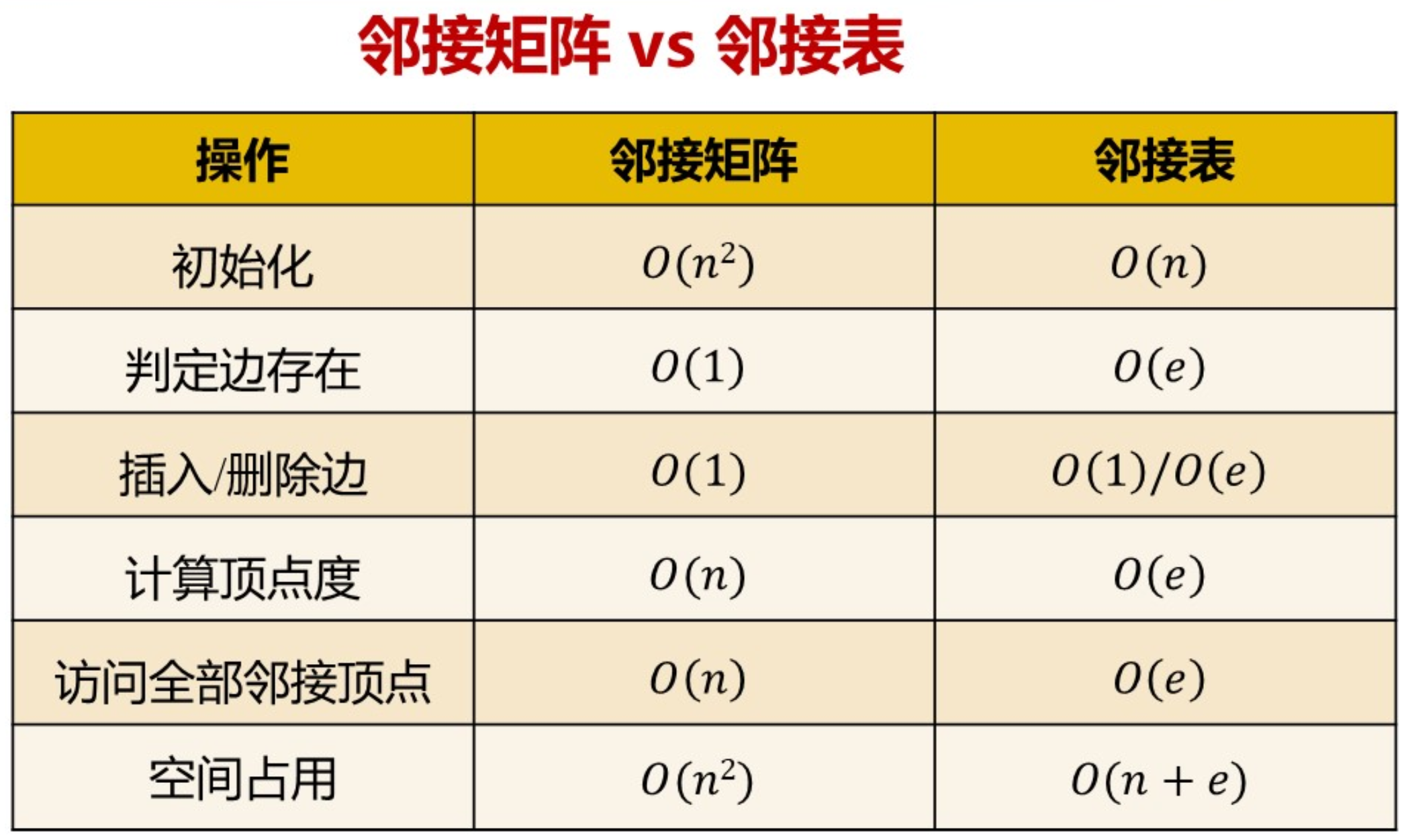
稠密图适于采用邻接矩阵表示
大规模的稀疏图$(e << n^2)$,适于采用邻接表表示
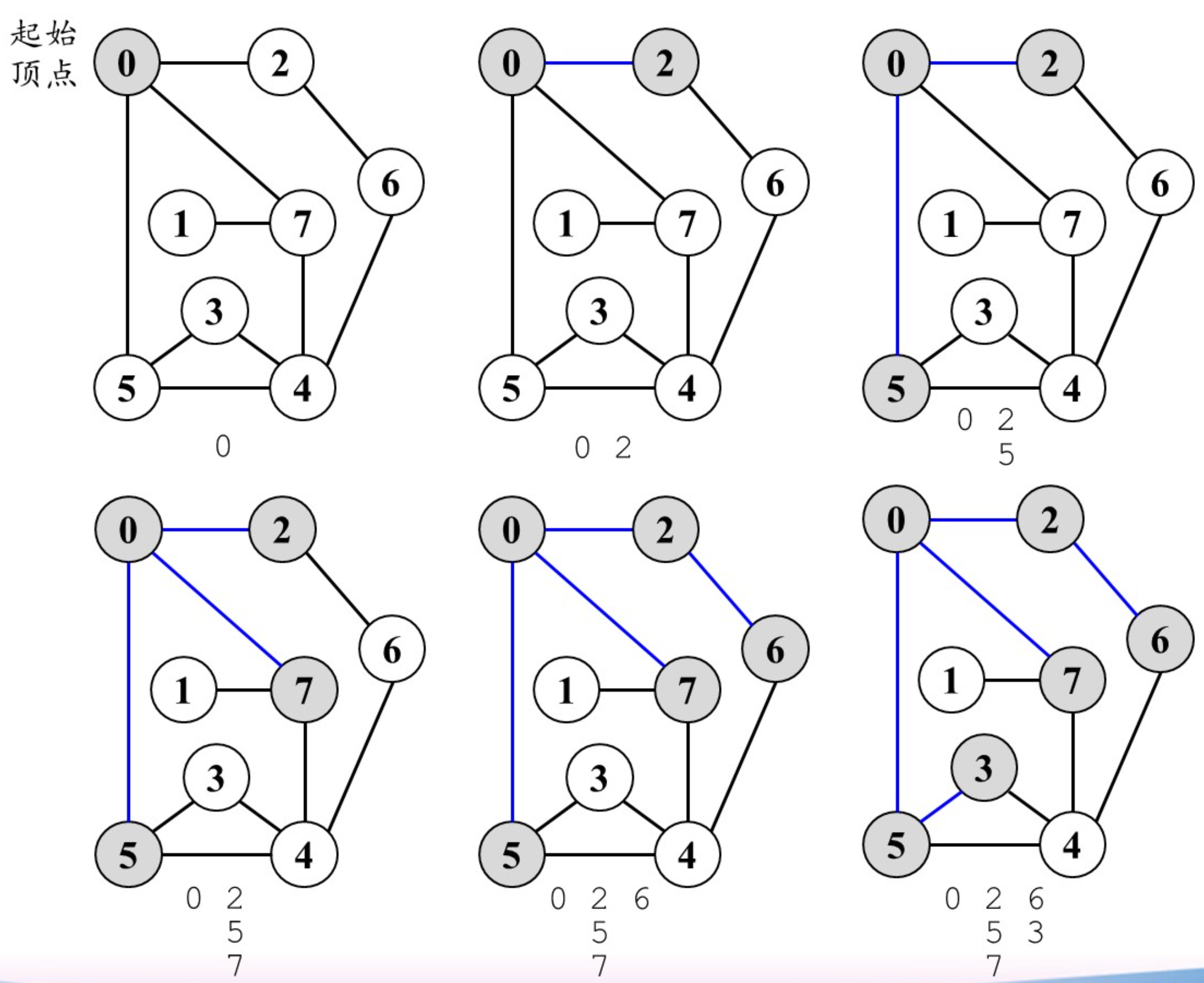
图的遍历
深度优先遍历(DFS)
深搜类似于二叉树的先序遍历
代码实现:1
2
3
4
5
6
7
8template <class ElemType>
void Graph<ElemType>::DFS(int v){
cout << v << ' ';
visited[v] = 1;
for(int t = FirstAdjVex(v); t != -1; t = NextAdjVex(v,t)){
if(visited[t] == 0) DFS(t);
}
}
稠密图适于在邻接矩阵上进行深度遍历;稀疏图适于在邻接表上进行深度遍历。
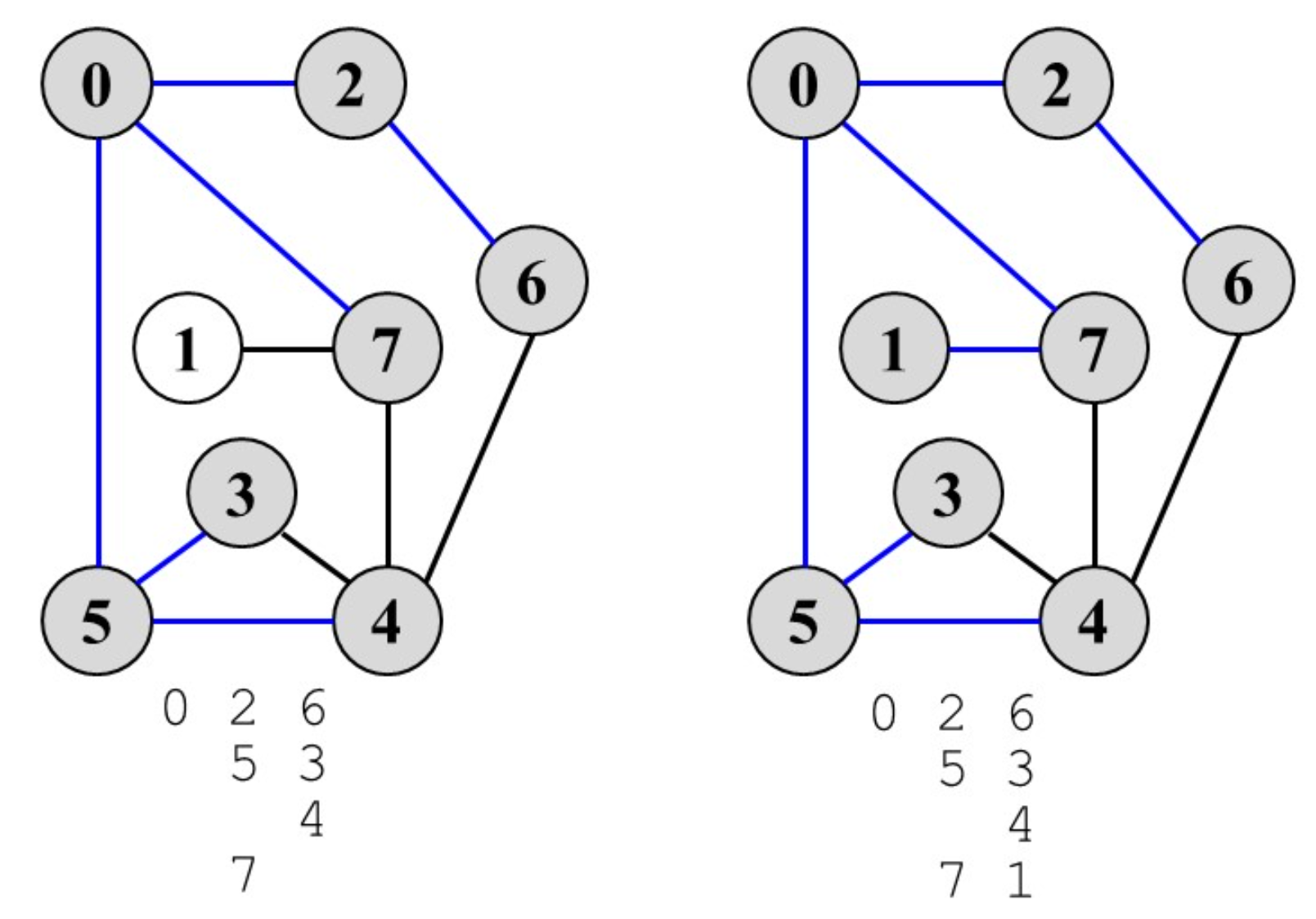
广度优先遍历(BFS)
类似层序遍历
算法效率分析
时间复杂度:
用邻接矩阵来表示图时,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度为$O(n)$,总共是$O(n^2)$。用邻接表来表示图时,虽然有$2e$个表结点,但只需扫描$e$个结点即可完成遍历,加上访问$n$个头结点的时间,时间复杂度为$O(n+e)$。
图遍历的应用
- 寻找图中从顶点$v$到顶点$w$的简单路径
使用DFS,路径删除规则:维护一条路径P依次记录DFS中访问的顶点,如果某顶点全部邻接点均被访问仍没有到达$w$,则从路径中删除此顶点;最终到达$w$时,路径中记录的即为从$v$到$w$的一条简单路径
下图中的1和3满足路径删除规则: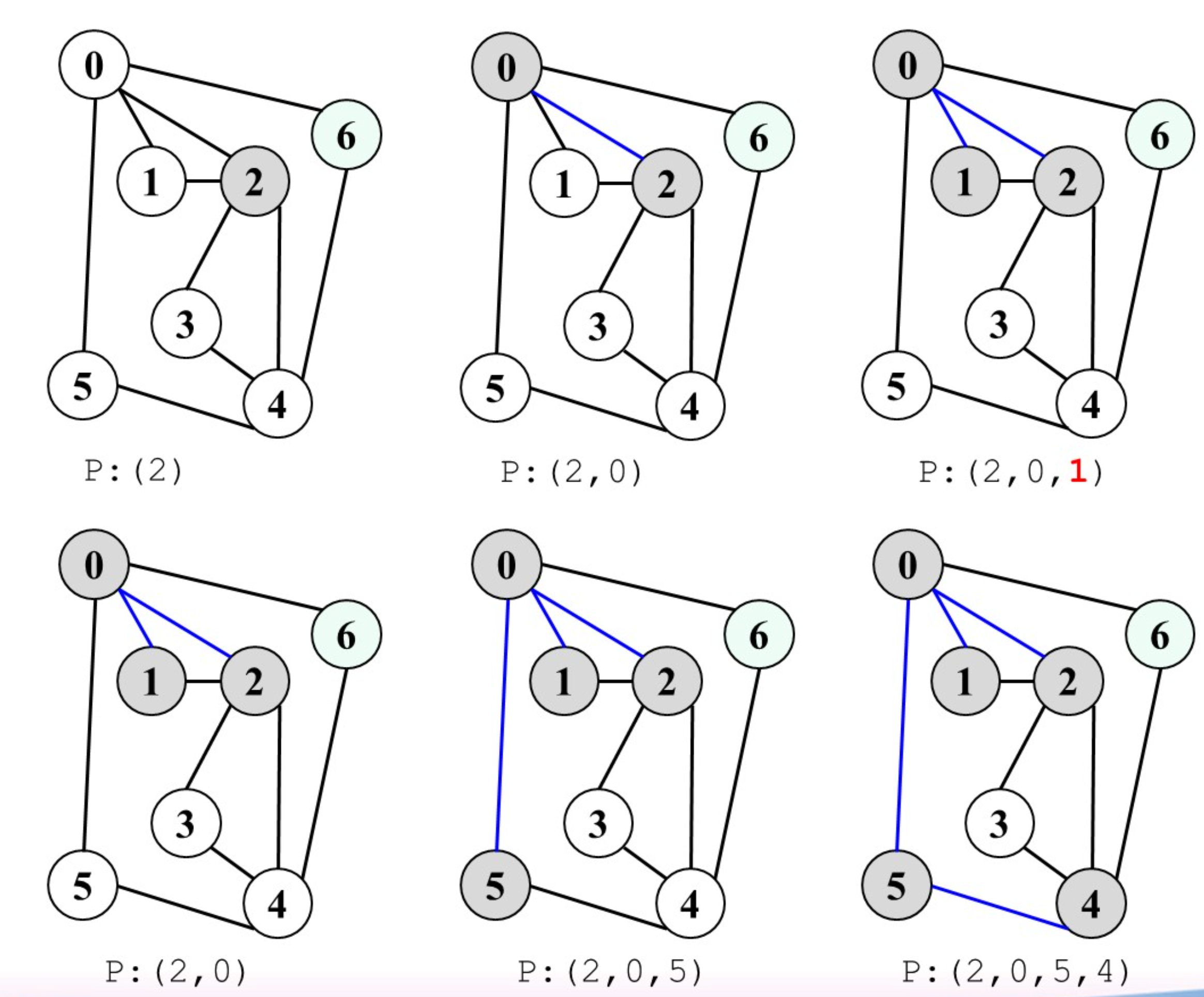
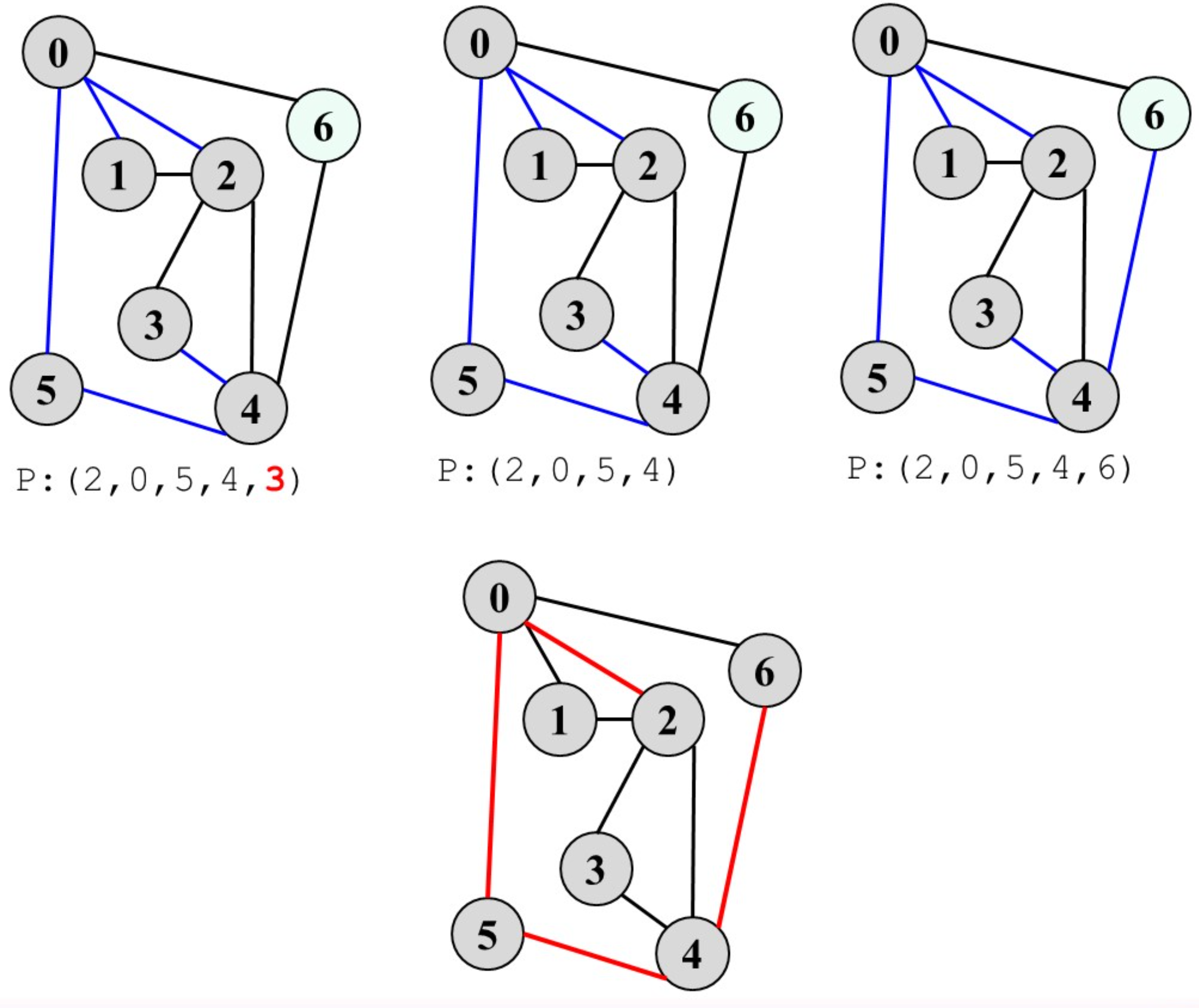
- 无权图中从顶点$v$到顶点$w$的最短路径
使用BFS
遍历与图的连通性
关节点与桥:
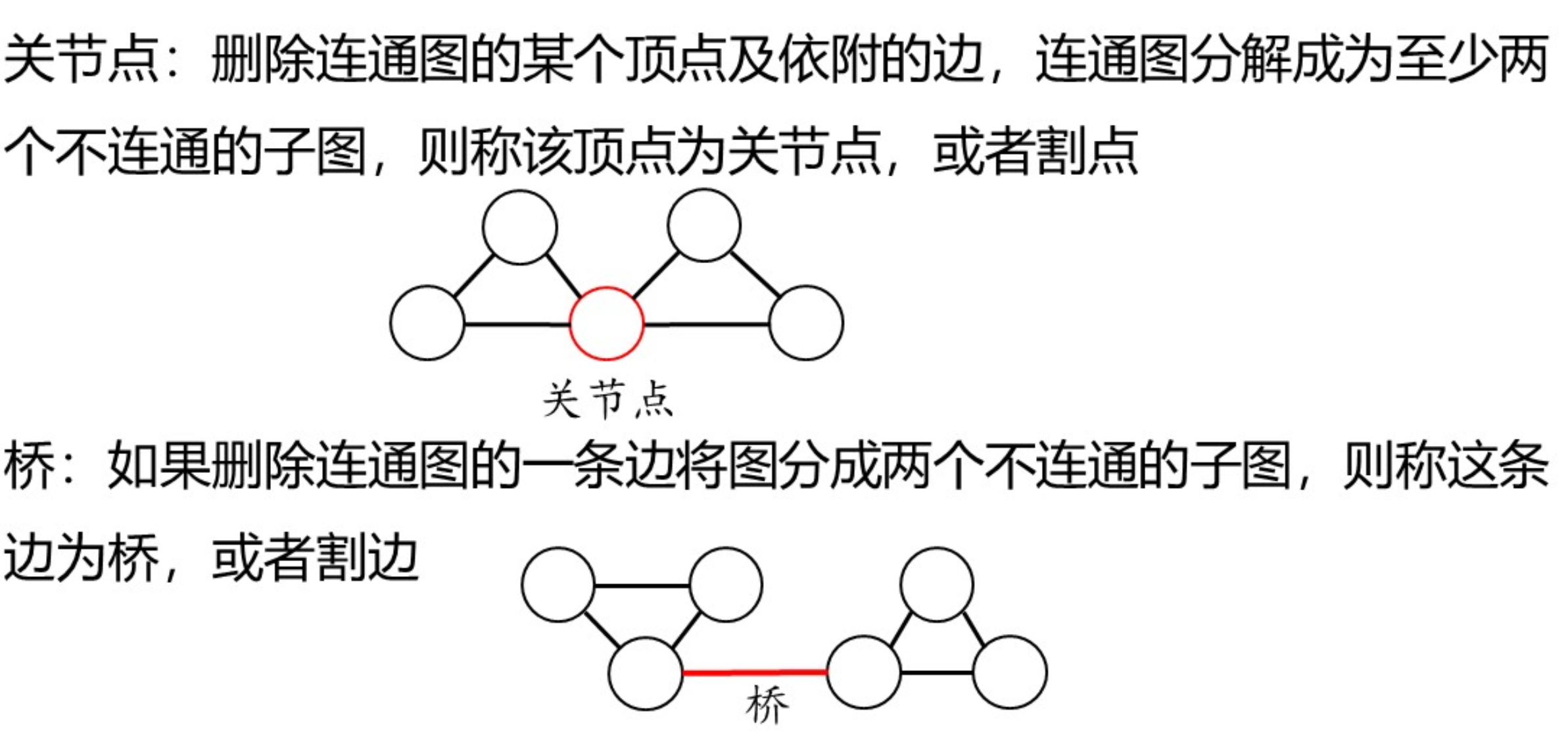
注意:无向连通图的顶点度都为偶数,则该图没有桥
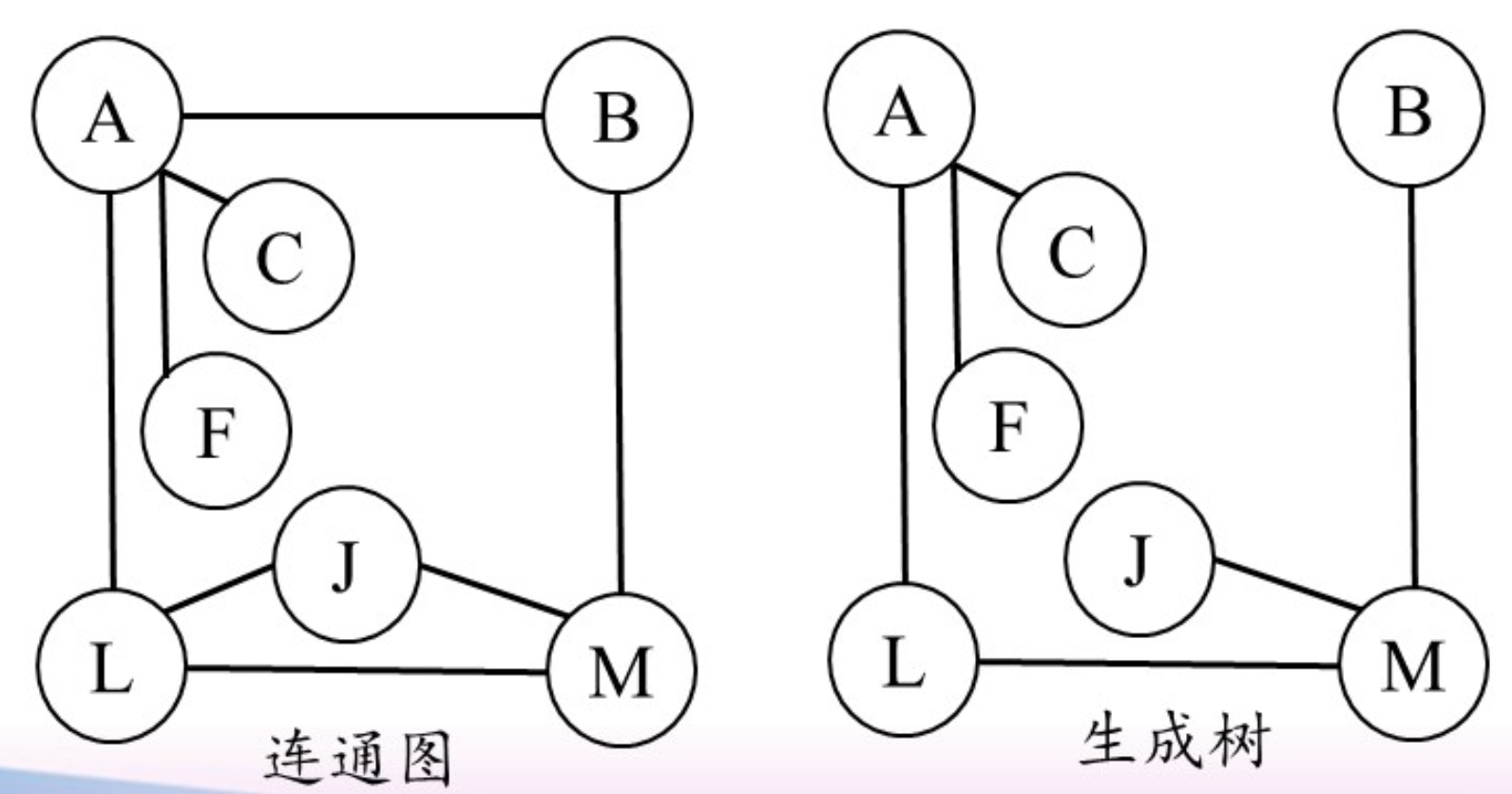
最小生成树
无向连通图的生成树:包含图中全部n个顶点,但仅有 $n-1$ 条边的连通子图
满足以下条件:
- 生成树上删除一边则不再连通
- 生成树上添加一条边则一定会产生回路
- 生成树可以理解为’极小’连通图,且可以不唯
最小生成树:
- 赋权图生成树的权:组成生成树的 $n-1$ 条边的权之和
- 生成树的权不大于其它任何生成树,称为最小生成树
- 如果图中有相等权值的边,则MST可能不唯一
Prim算法
本质上是一种贪心算法,每次选择权值最小的边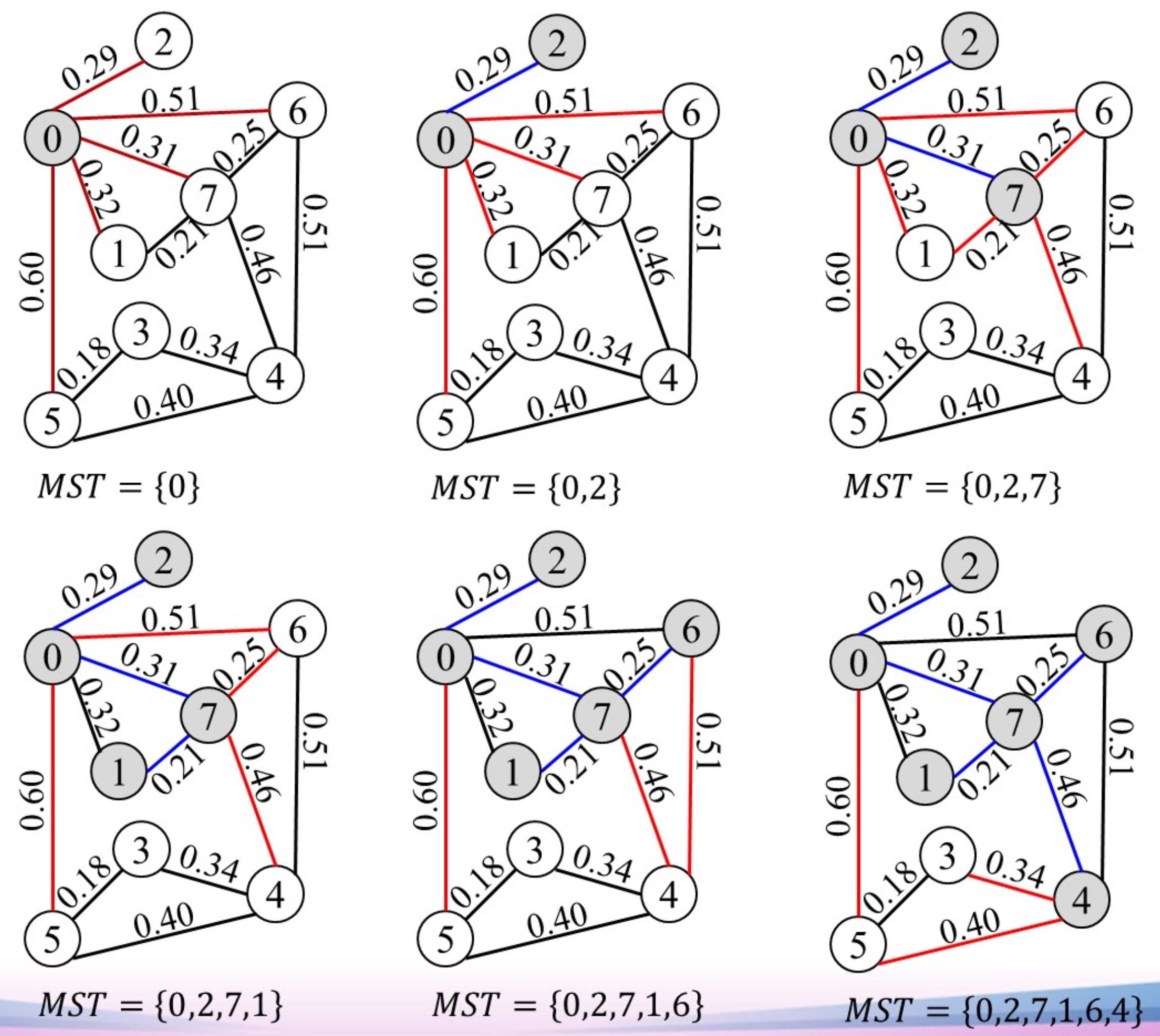
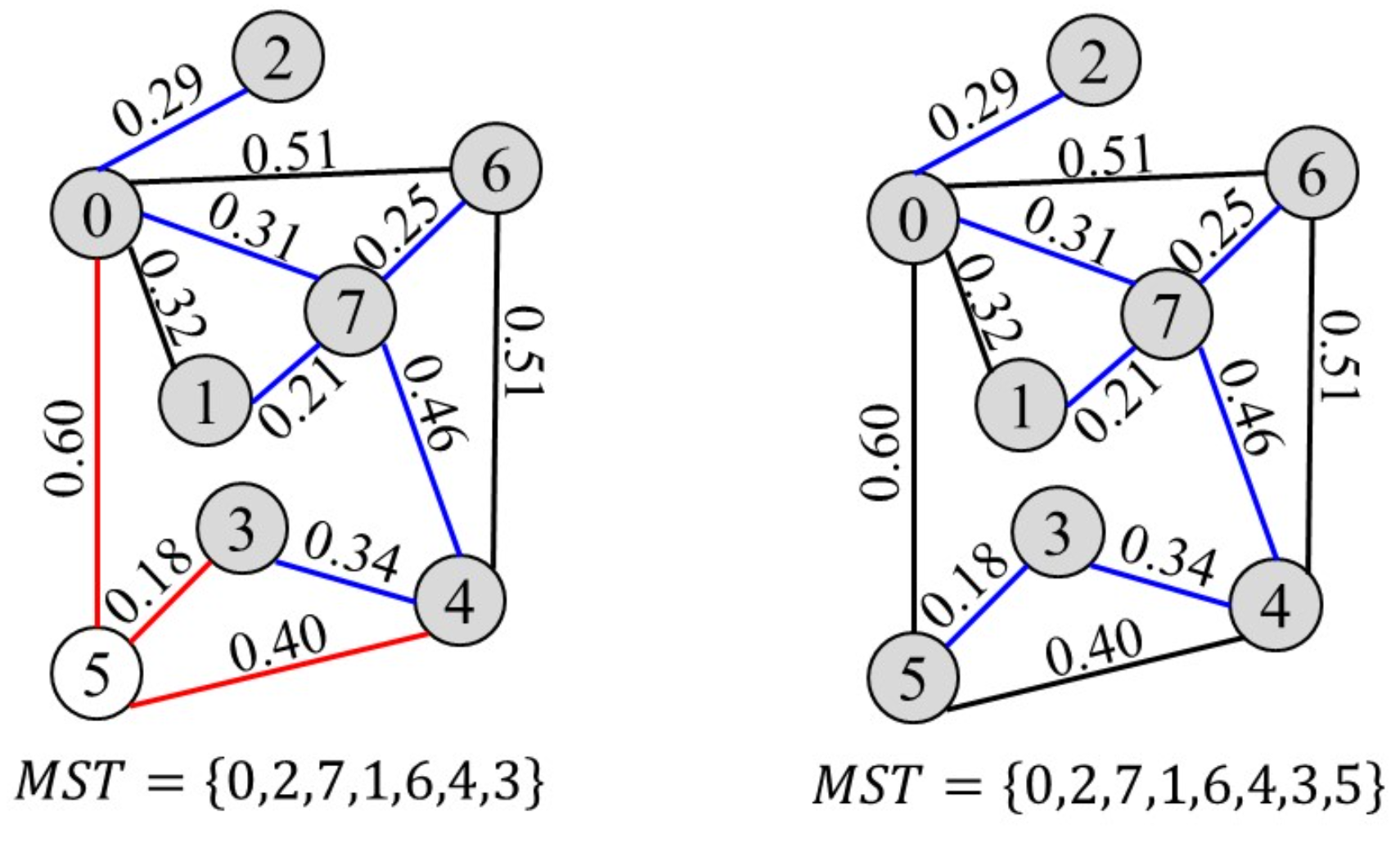
对于邻接矩阵和邻接表来说,时间复杂度都为 $O(n^2)$
这是因为:每次迭代需要遍历所有 $n$ 个顶点来寻找最小权重边,找到新顶点后,需要遍历邻接矩阵中该顶点的所有 $n$ 个邻接点来更新权重,总时间 $O(n^2)$
为什么Prim算法得到的一定是MST?
Prim算法一定能得到最小生成树(MST)的根本原因在于其设计严格遵循了MST的两个核心数学性质,并通过贪心策略保证每一步选择的边都安全地属于MST。以下是详细解释:
1. 切割定理(Cut Property)的保证
Prim算法的核心逻辑是:每次选择连接”已选顶点集合(MST部分)”与”未选顶点集合”的最小权重边。
切割定理:若将图划分为两个顶点集合(例如已选集合$U$和未选集合$V-U$),则连接这两个集合的最小权重边一定属于MST。
算法行为:每次选出的边,本质上就是当前切割(已选顶点与未选顶点之间的分割)的最小权重边。2. 无环性的维护
顶点增量扩展:算法每次仅将一个新顶点加入已选集合$U$且该顶点从未属于$U$。
边连接方式:新加入的边始终连接$U$和$V-U$,不会在$U$内部形成回路,也不会在$V-U$内部形成回路。
树形结构保持:已选边集始终构成一棵树(无环且连通),直到覆盖所有顶点。3. 贪心策略的全局最优性
局部最优蕴含全局最优:通过归纳法可证明,每次选择的局部最优边最终能组合成全局最优解:
初始状态:空树是MST的平凡情况(权值和为0)。
归纳假设:假设前k步已选择的边构成某棵MST的边子集。
递推步骤:根据切割定理,第k+1步选择的边必然属于某棵MST,最终所有顶点加入后,整体构成MST。
Kruskal算法
也是一种贪心算法,重要特征是放弃环路.环路的判断采用等价类思想(并查集),将已连通的顶点均用其中一个顶点代表
算法步骤:
算法复杂度为:$O(eloge)$
最短路径
一些特点:
- 最短路径存在的充要条件:图中不存在负环。
- 正权图中,如果存在最短路径,则一定不包含环
- 最短路径中任意一段也是局部最短路径(整体最优蕴含了局部最优)
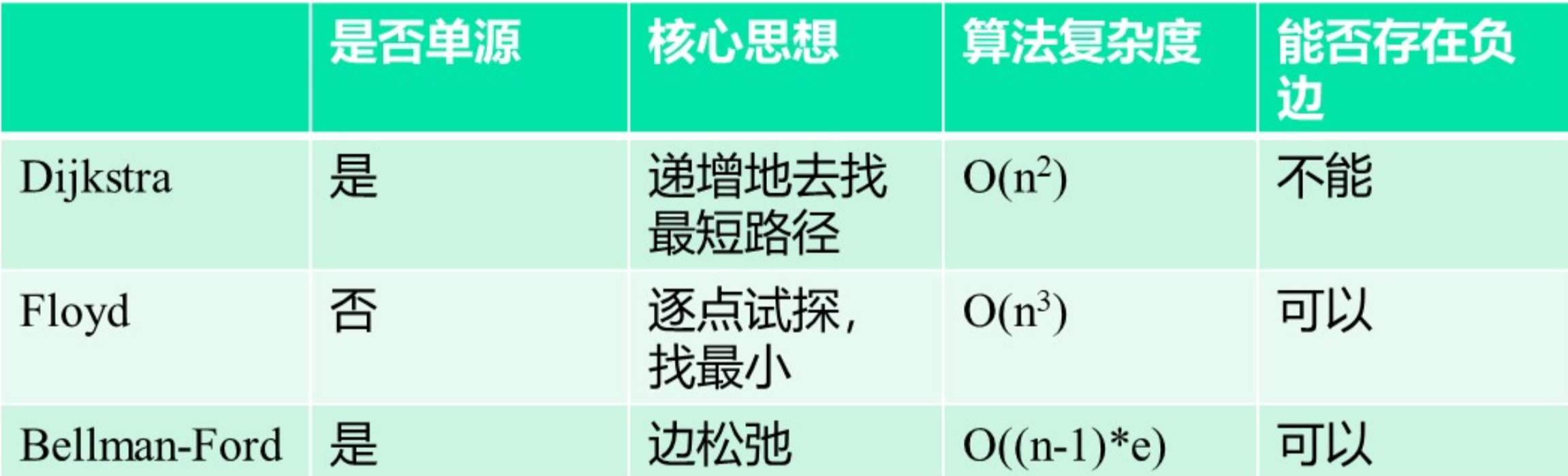
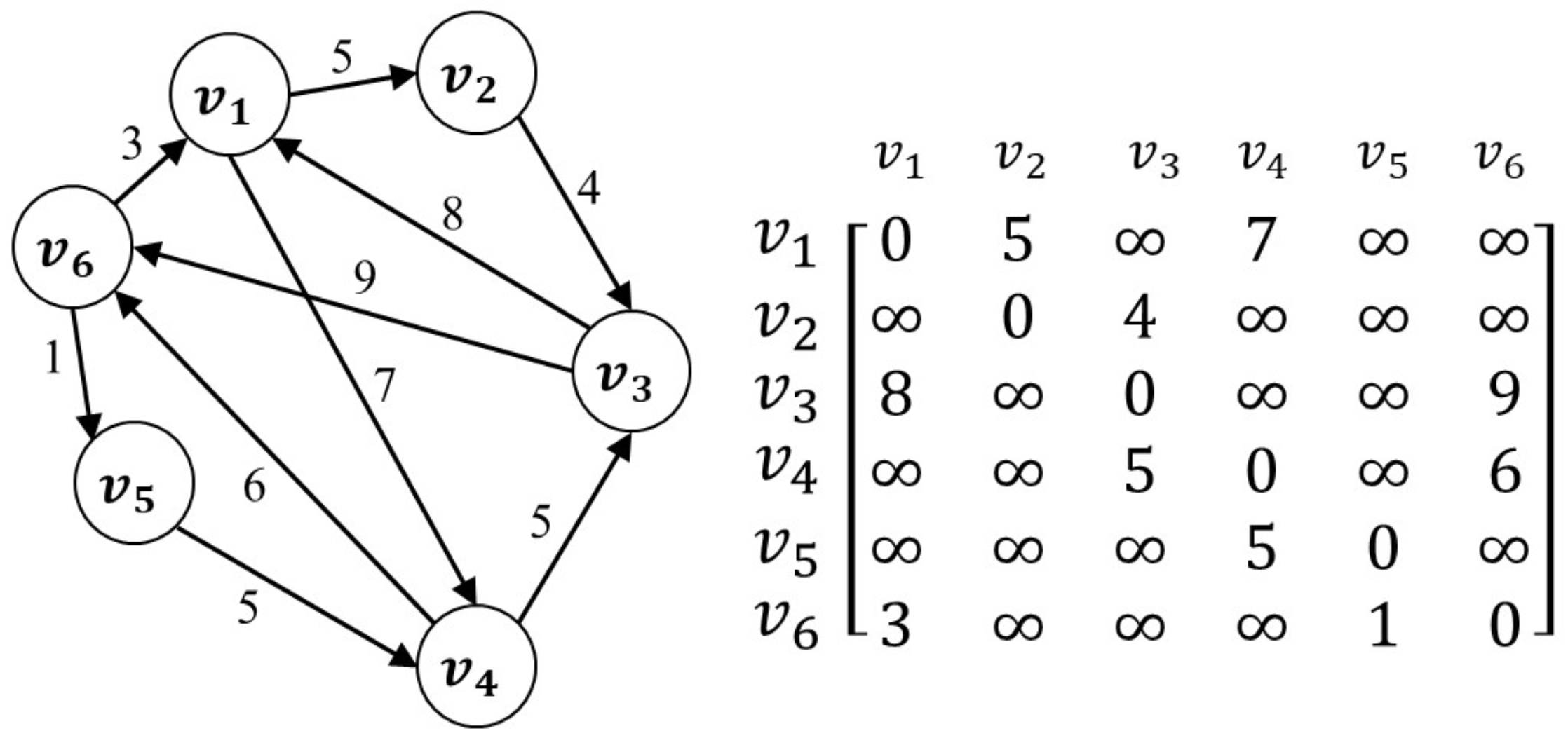
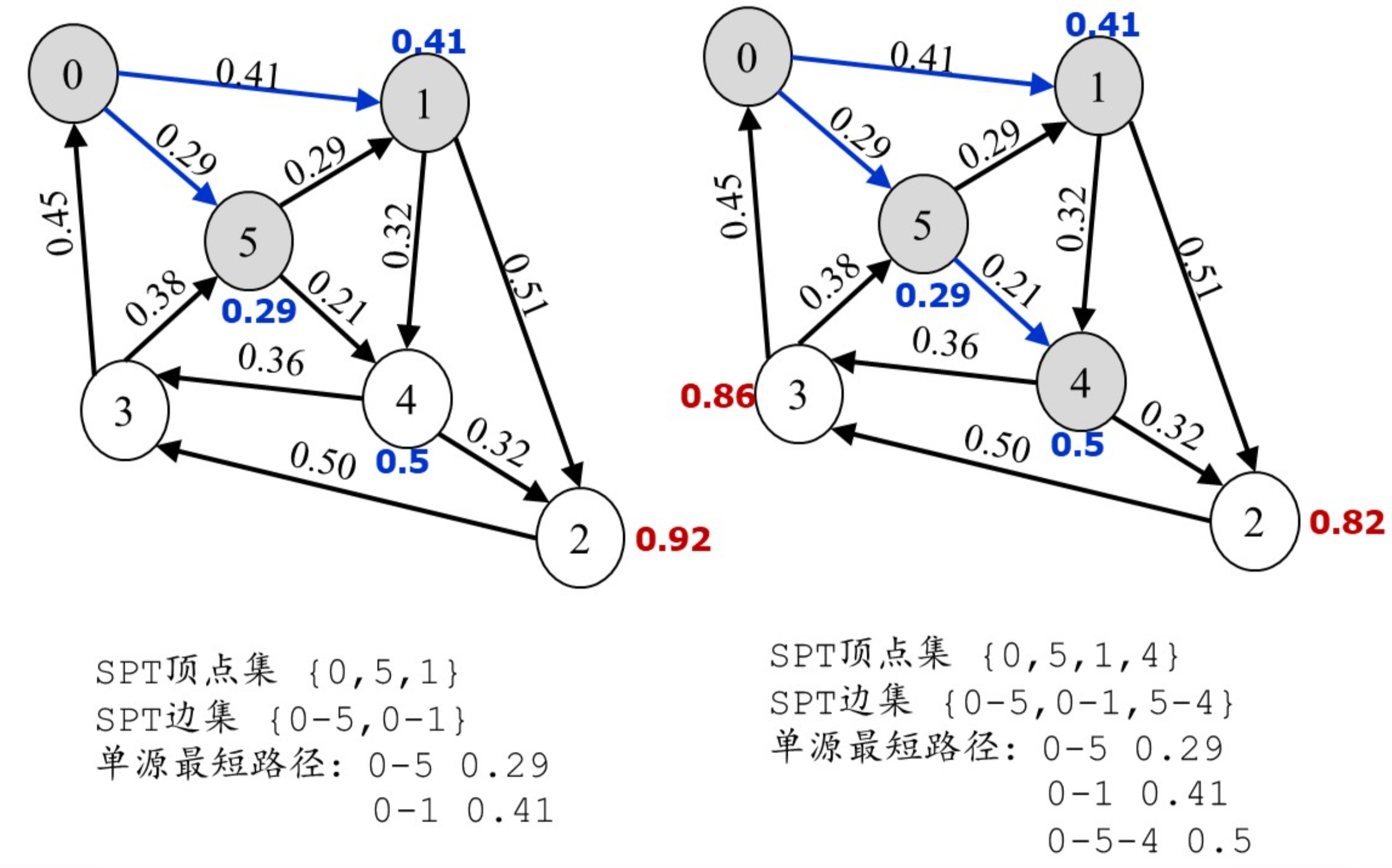
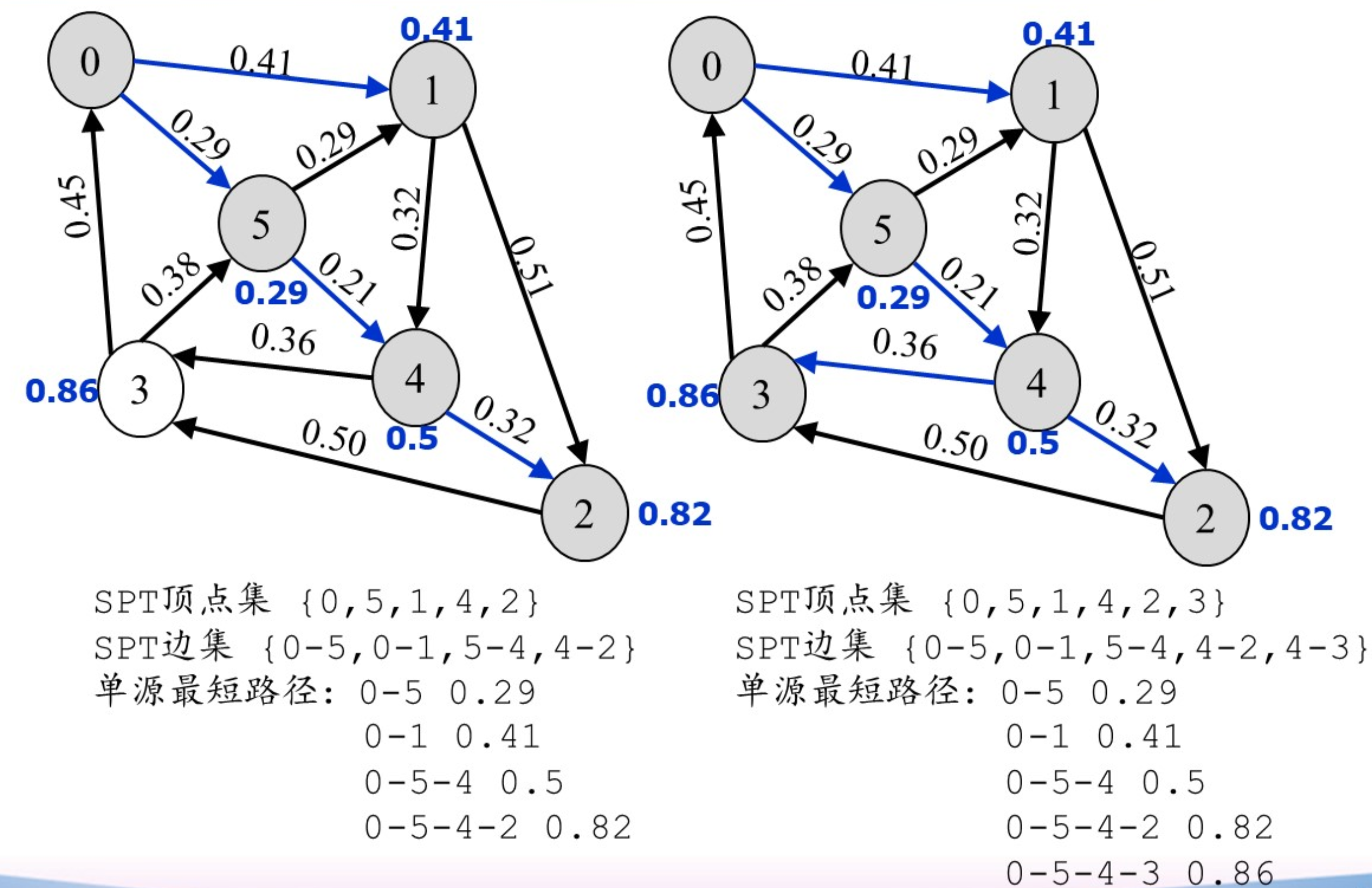
Dijkstra算法(单源最短路径)
算法的时间复杂度为:$O(n^2)$

图示: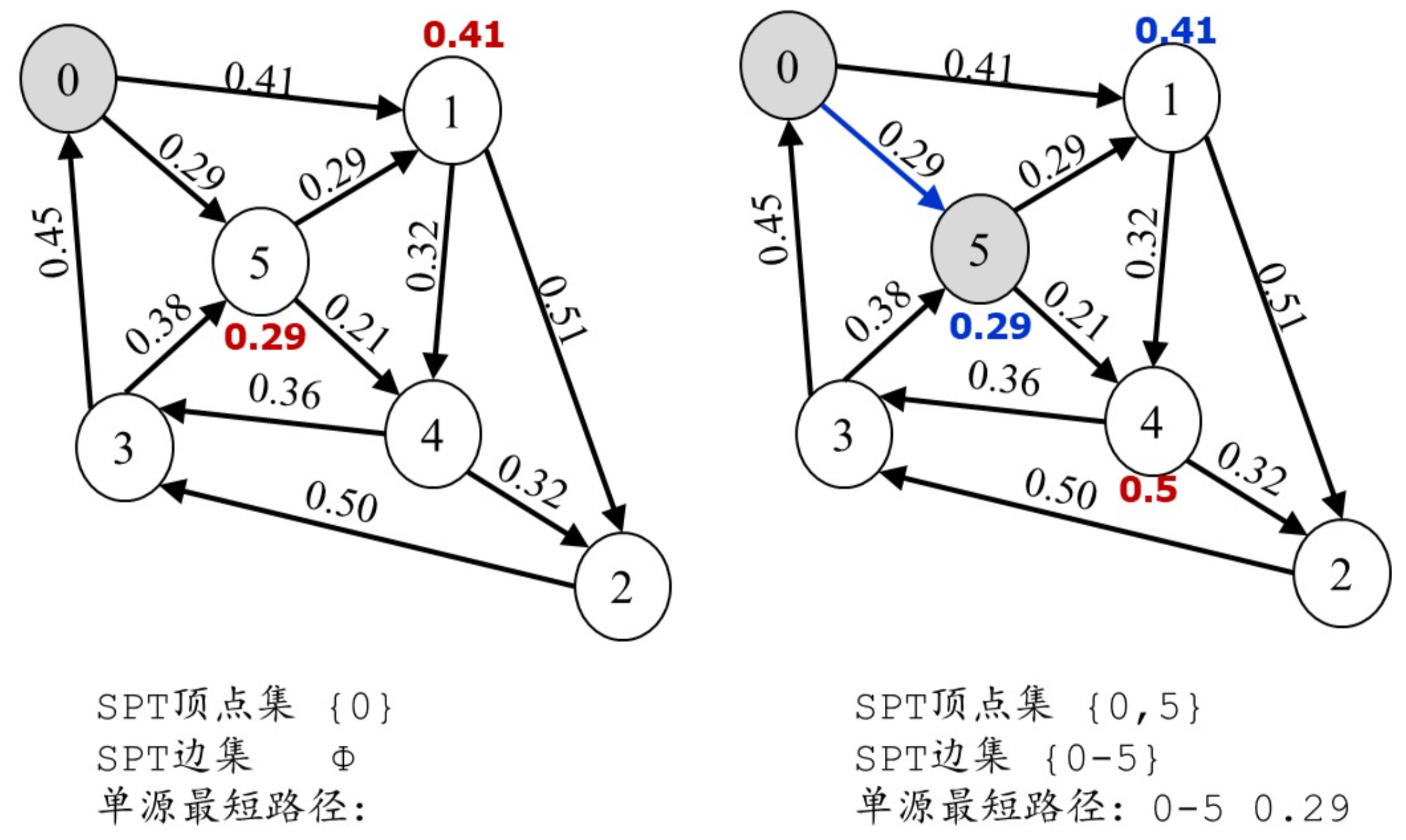
Floyd算法(全源最短路径)
若对每个顶点使用Dijkstra算法,则算法复杂度为$O(n^3)$
Floyd算法的复杂度也为$O(n^3)$,但是它允许负权边,不允许包含负回路
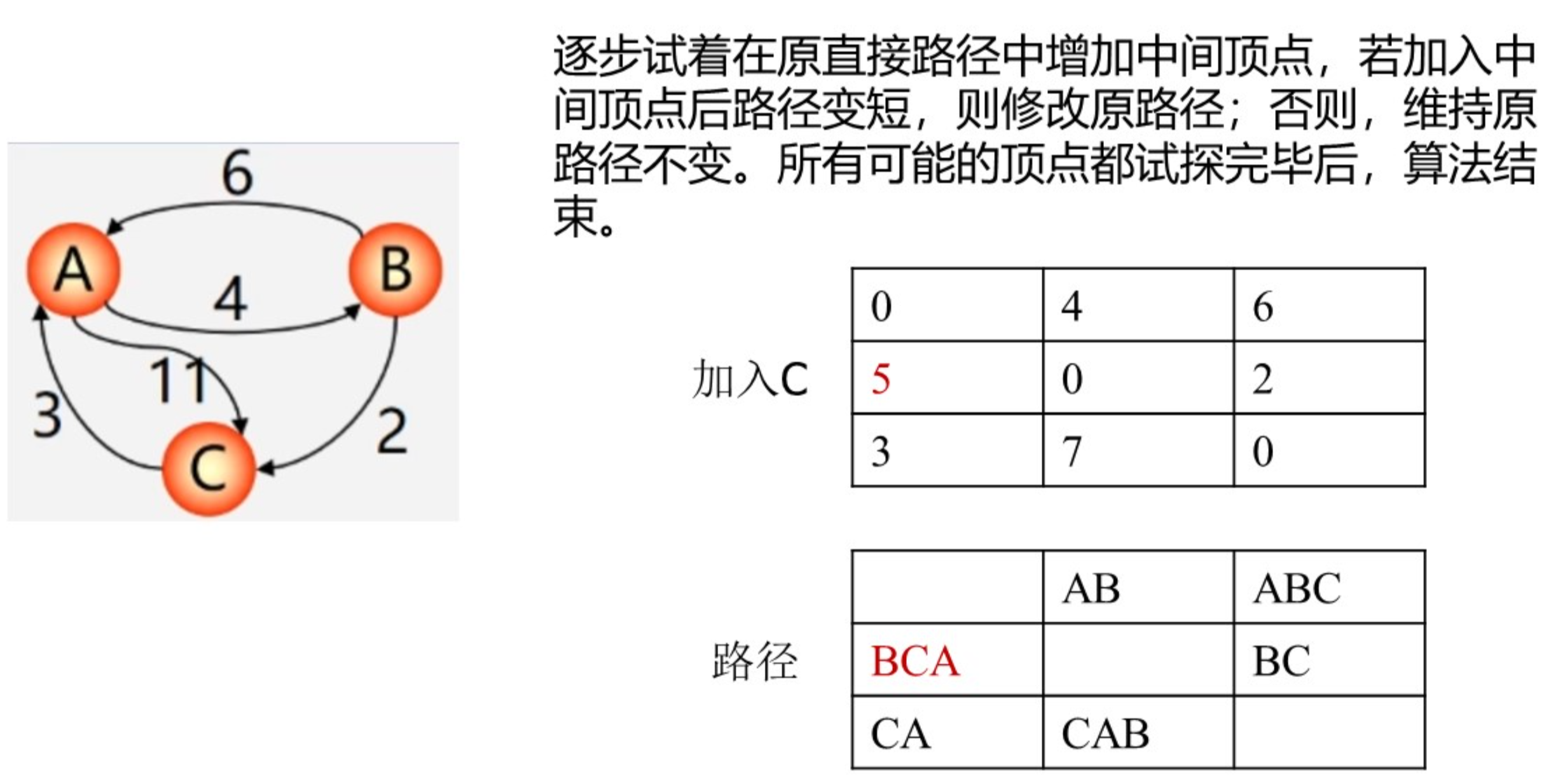
算法思想:
比如: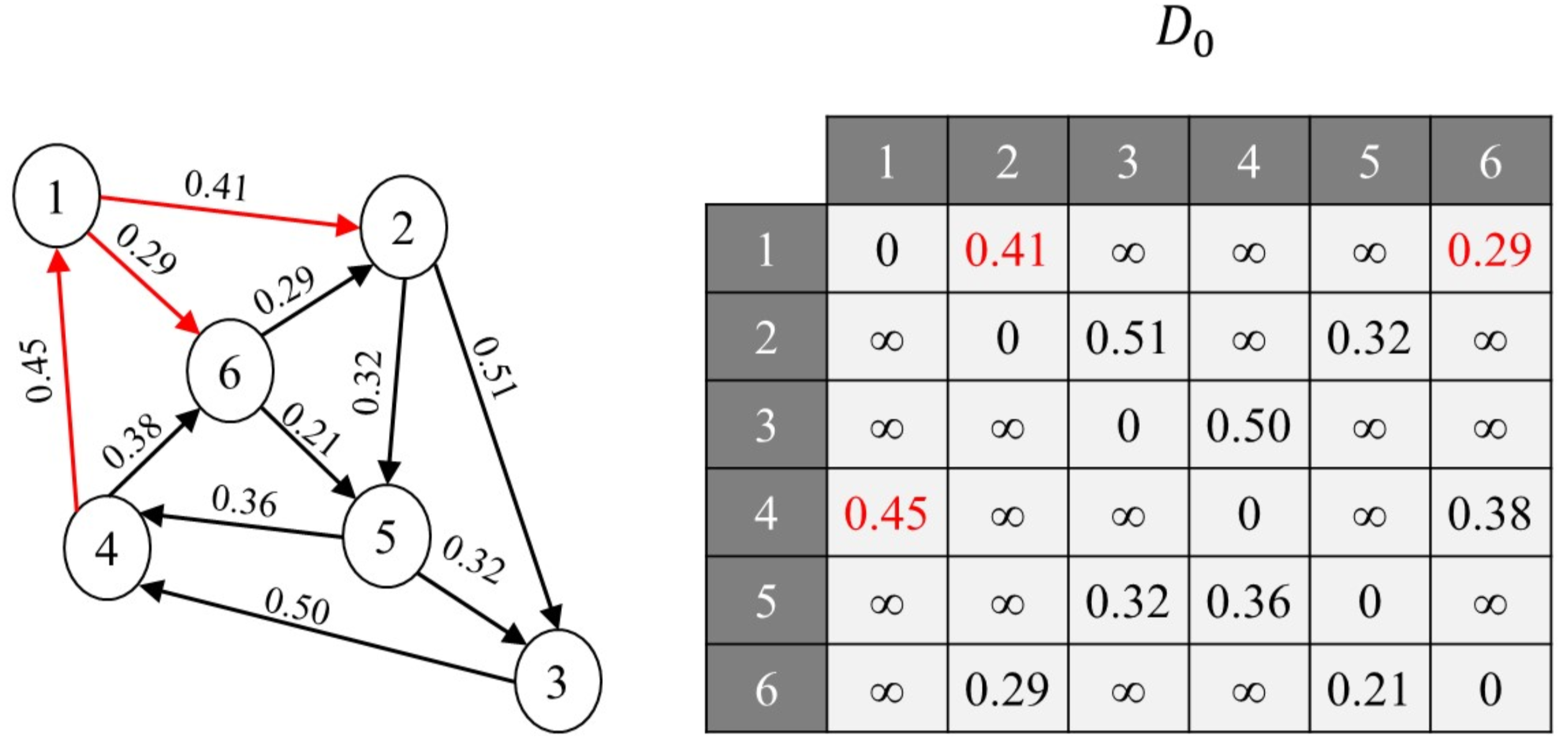
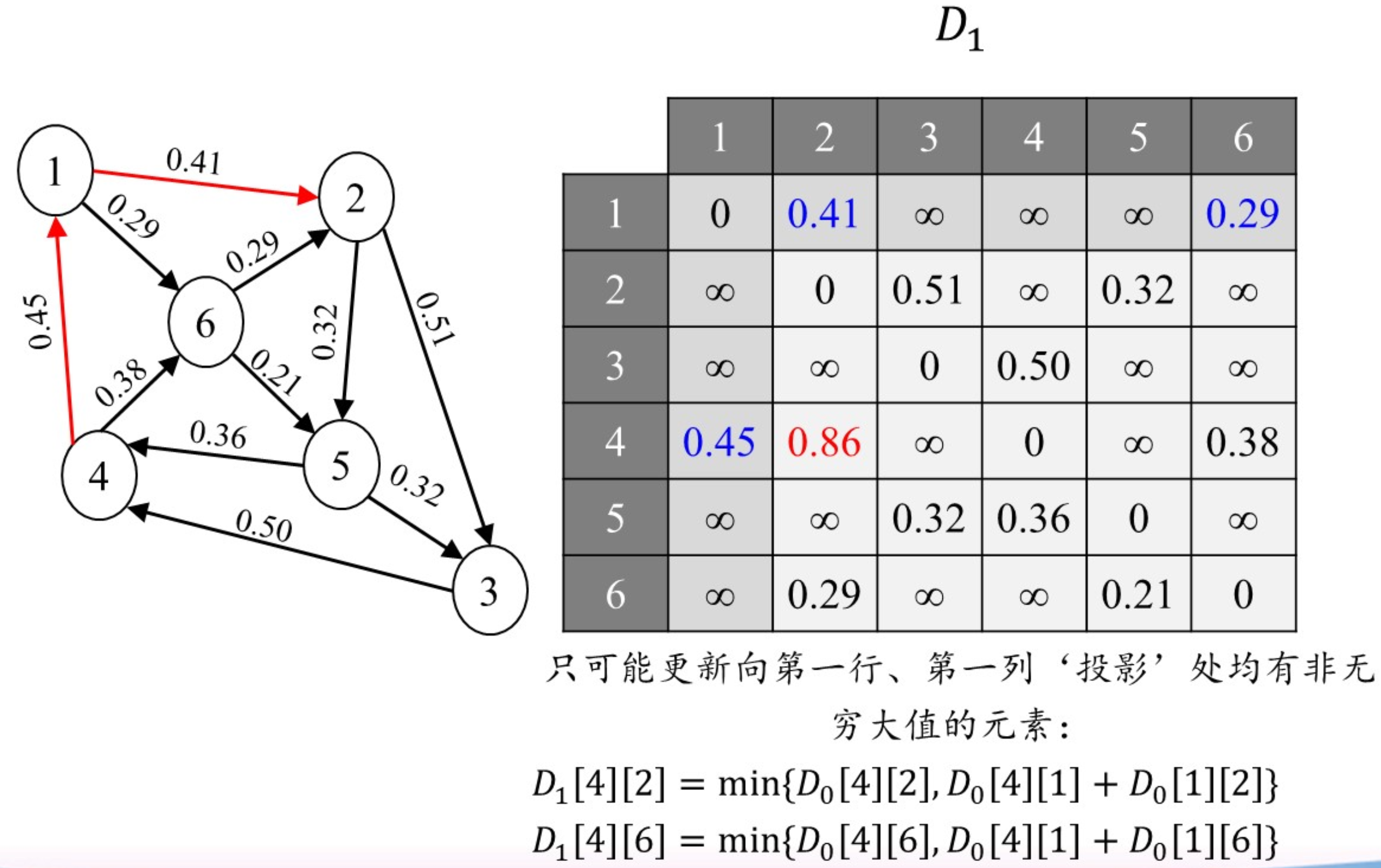
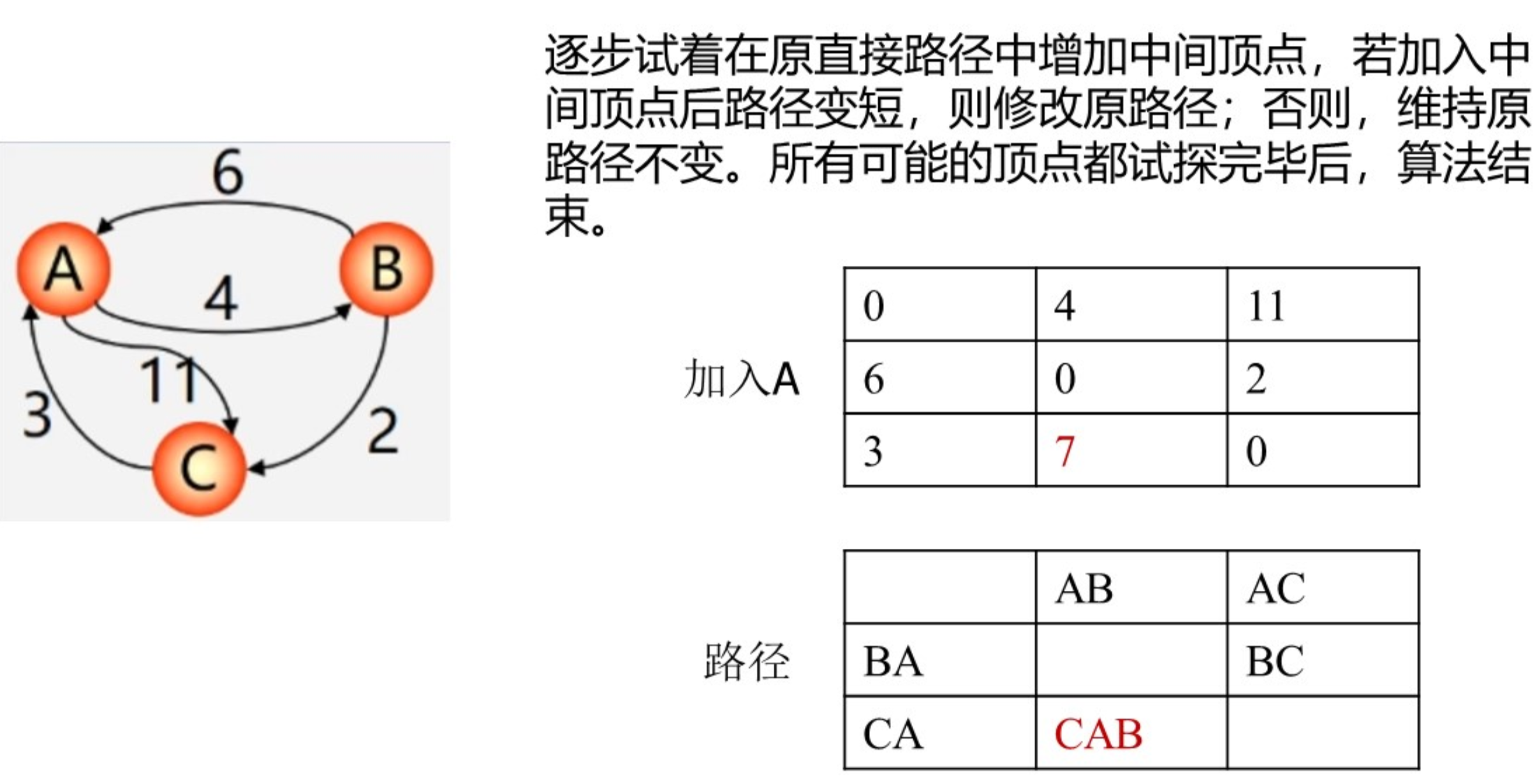
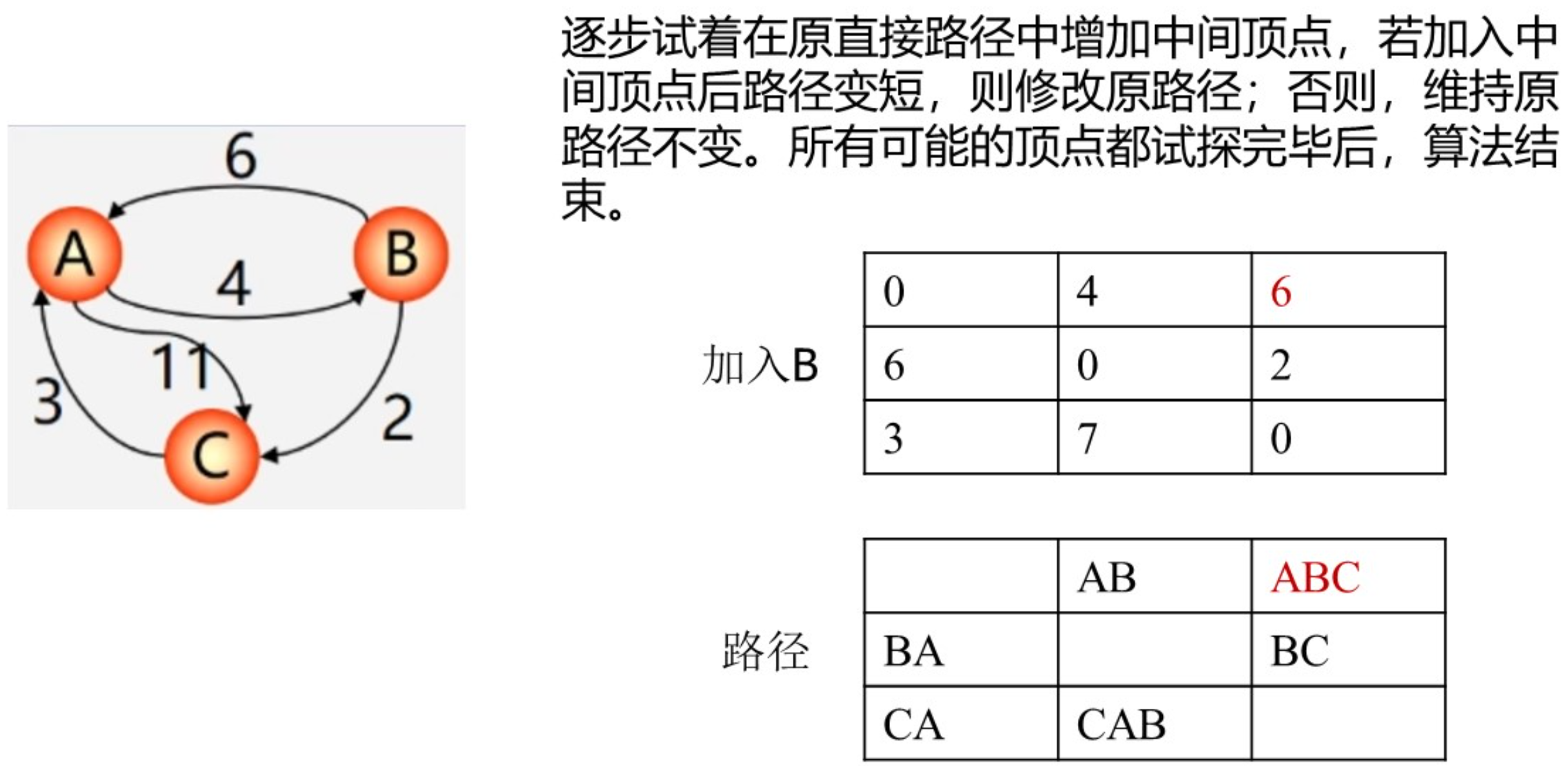
或者采用逐步加入顶点的思想来理解: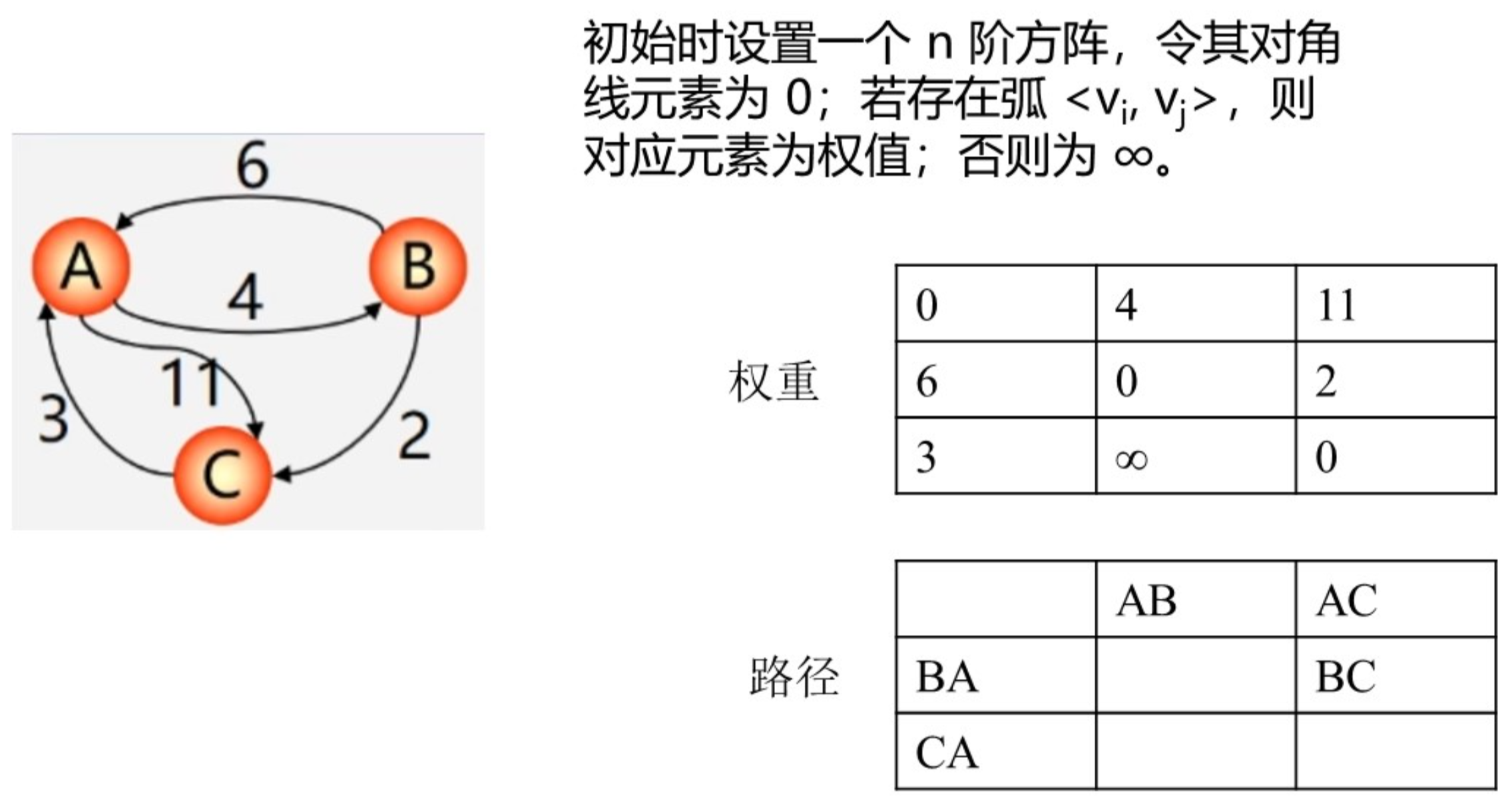
Bellman-Ford算法
重要思想:边松弛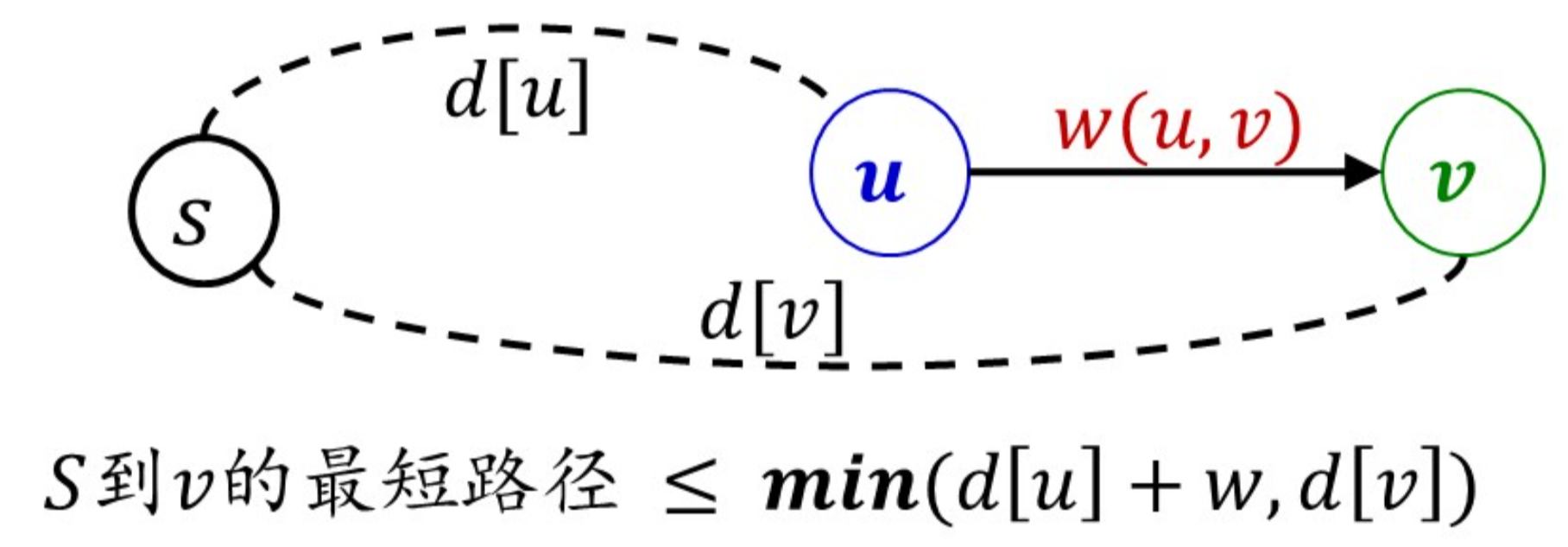
比如: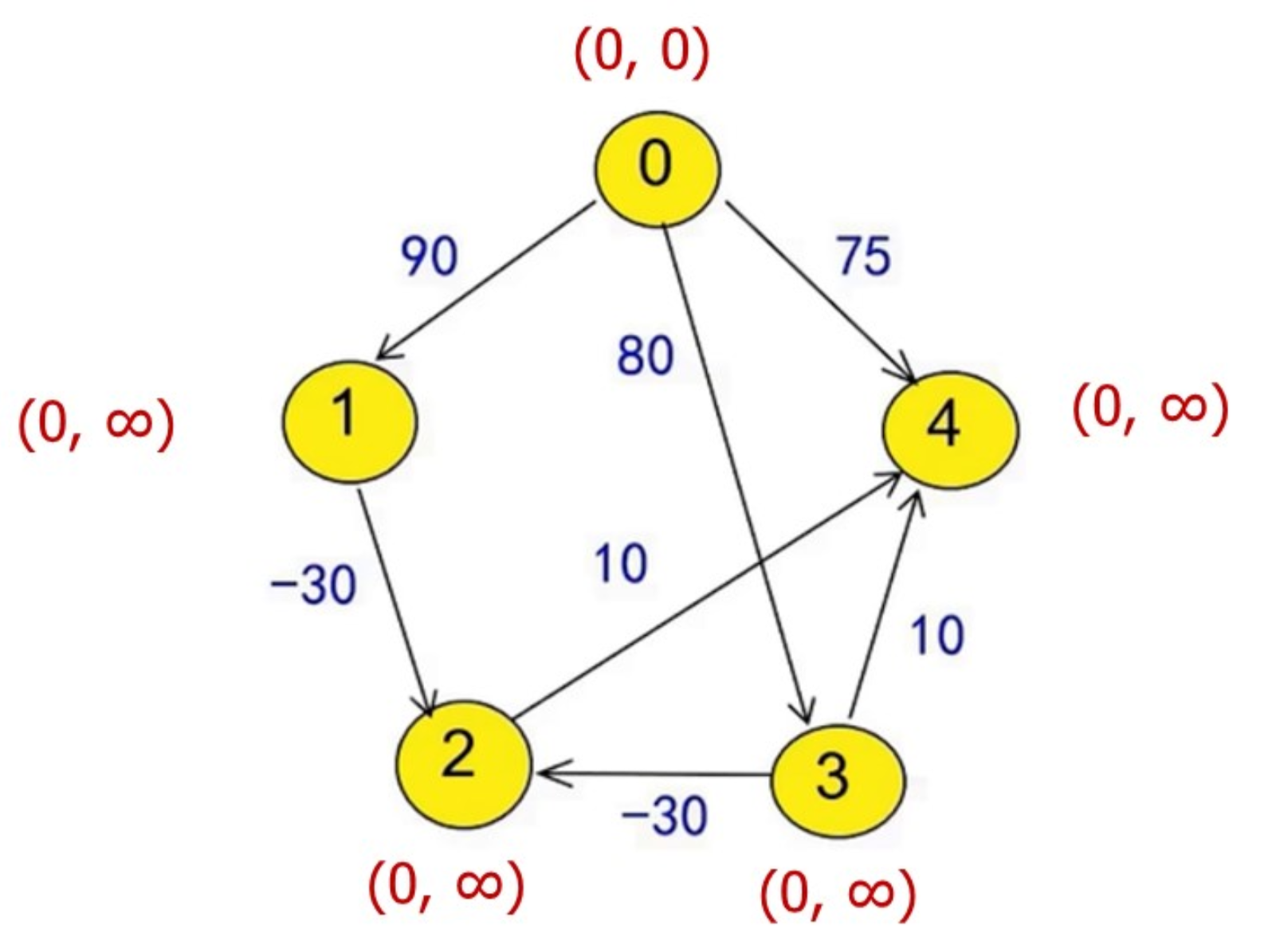
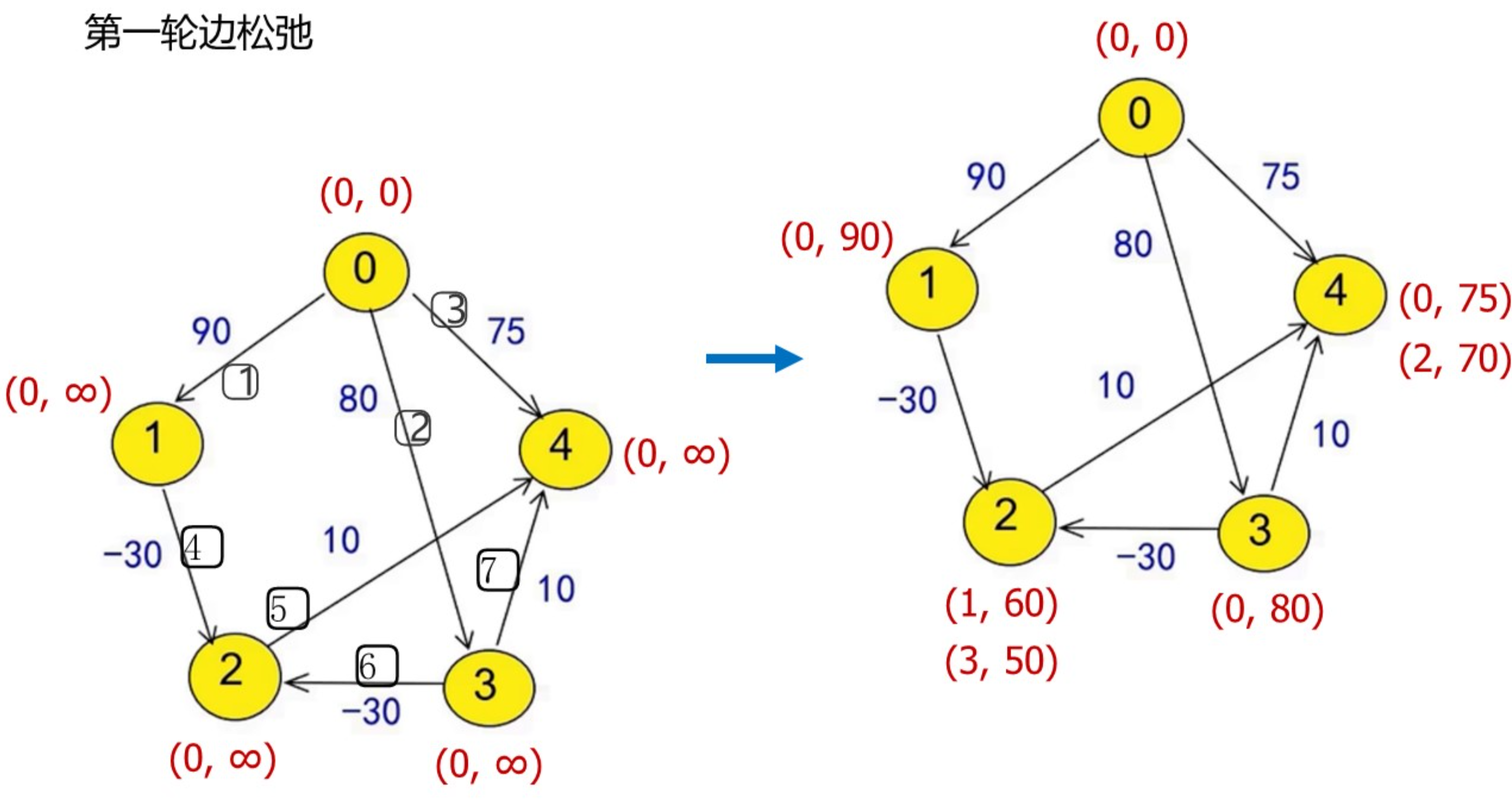
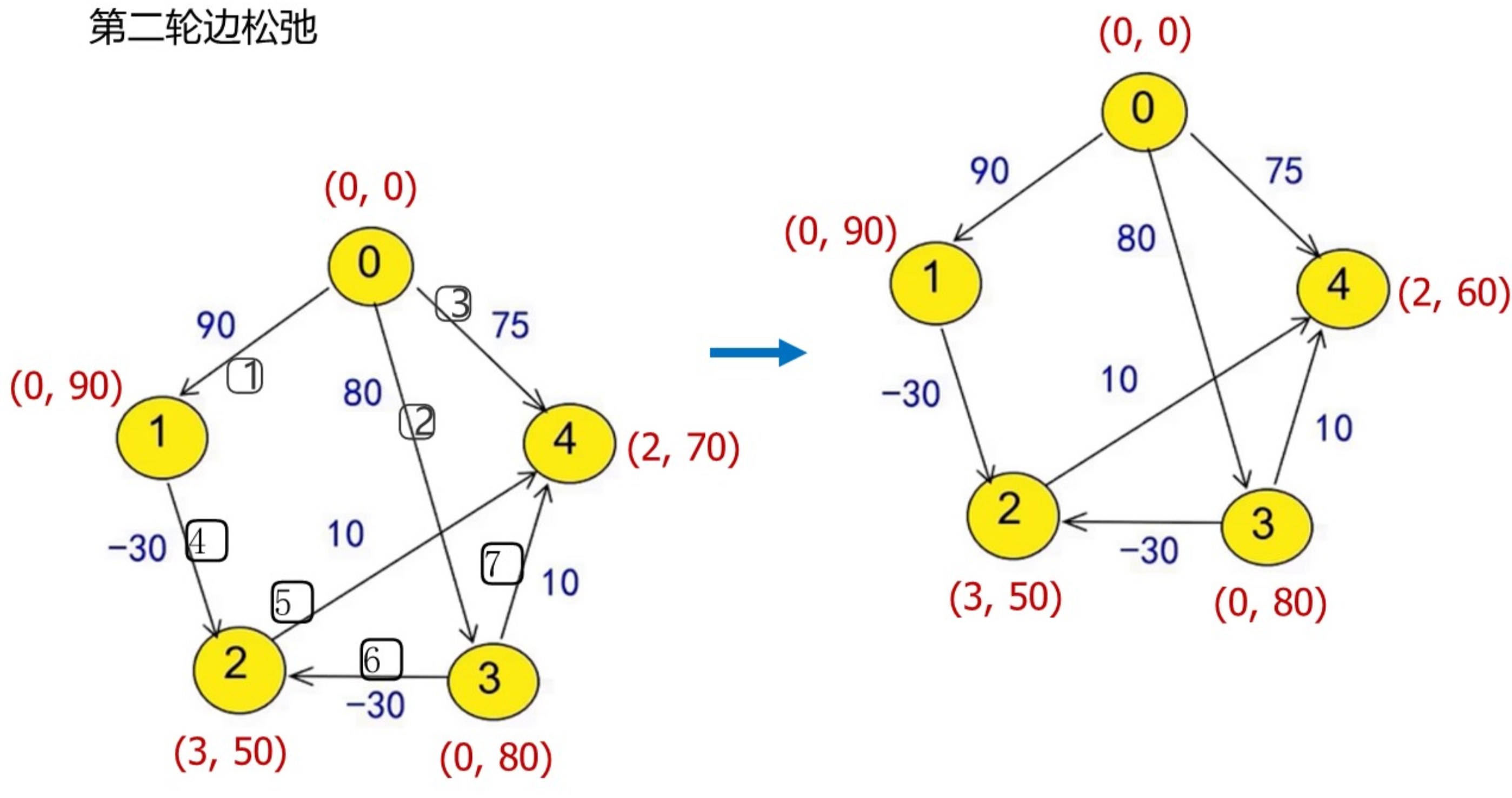
算法对比