查找与排序

发表于 更新于 阅读次数： 本文字数： 955 阅读时长 ≈ 1 分钟
数据结构与算法——查找与排序

查找与排序

查找

顺序查找

普通顺序查找的ASL

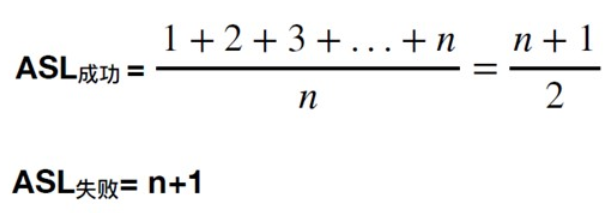
alt text

“哨兵”

待查找元素放在下标0处，从后往前找
优点：无需判断是否越界，效率高

有序表的ASL

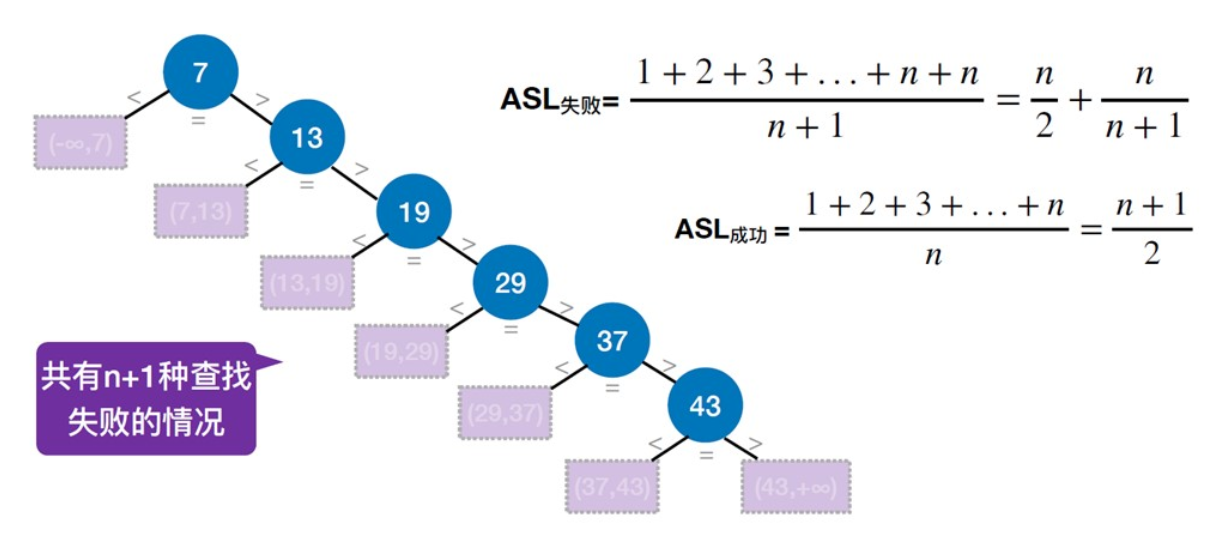
alt text

折半查找

折半查找速度最快
规避整数溢出的办法：int mid = low +((high - low)/2)

折半查找的判定树和ASL

mid放中间：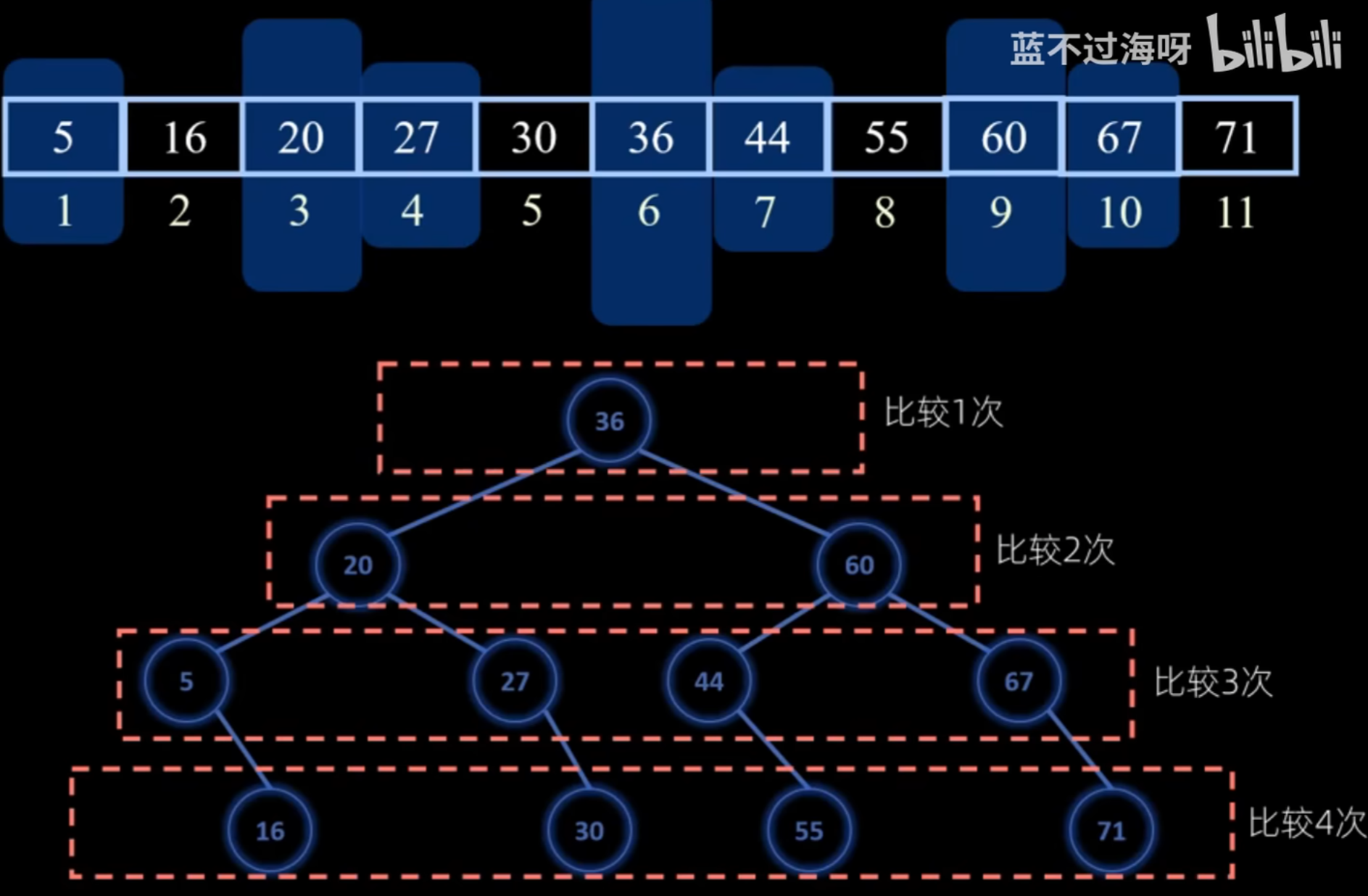
alt text

失败的只用比较层数-1：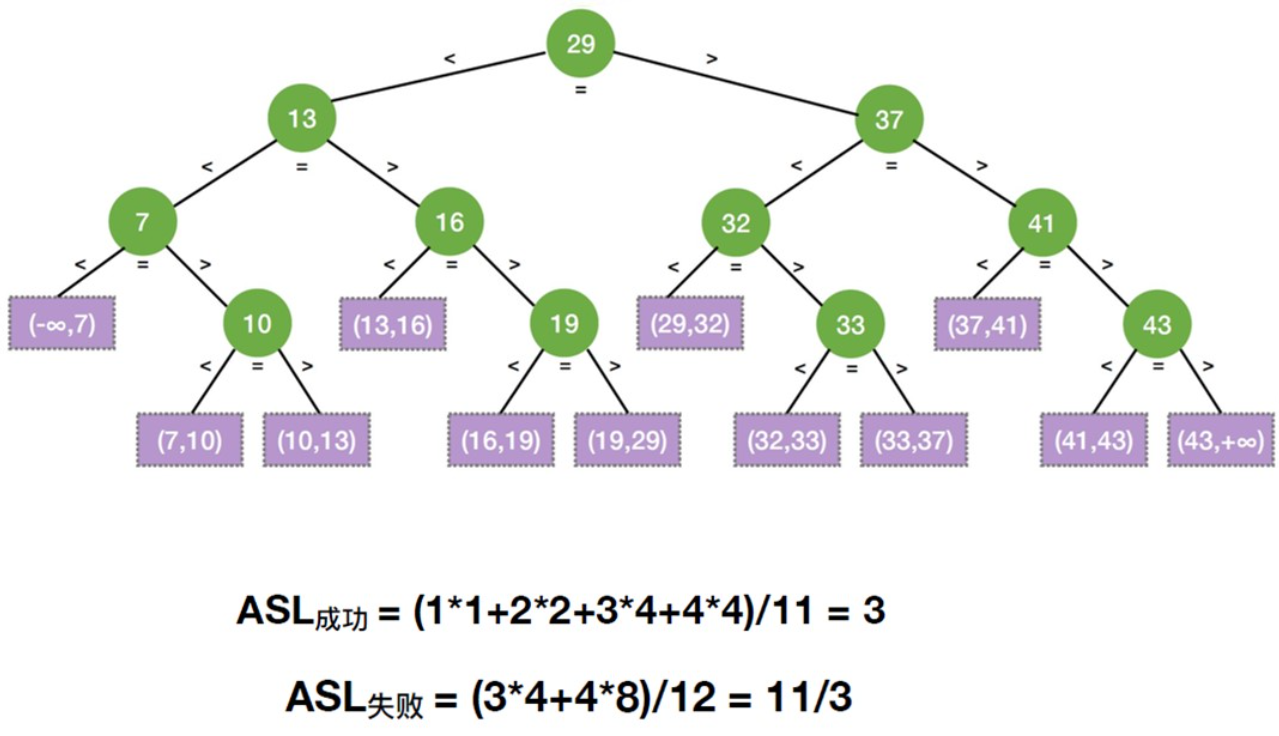
alt text

结构特点：

  1. 如果当前 low 和 high 之间有奇数个元素，则 mid 分隔后,左右两部分元素个数相等
  2. 如果当前 low 和high 之间有偶数个元素，则 mid 分隔后，左半部分比右半部分少一个元素
  3. 折半查找的判定树中，若 mid =[(low+high)/2]（向下取整），则对于任何一个结点，必有:右子树结点数-左子树结点数=0或1
  4. 折半查找的判定树一定是平衡二叉树，失败节点有 $n+1$ 个
  5. 折半查找的判定树中，只有最下面一层是不满的因此，元素个数为n时树高$[h=log_2(n + 1)]$，因此折半查找的时间复杂度为$O(log_2n)$

折半查找的速度不一定比顺序查找快：比如要查的就在最开始的位置

二叉搜索树

构造

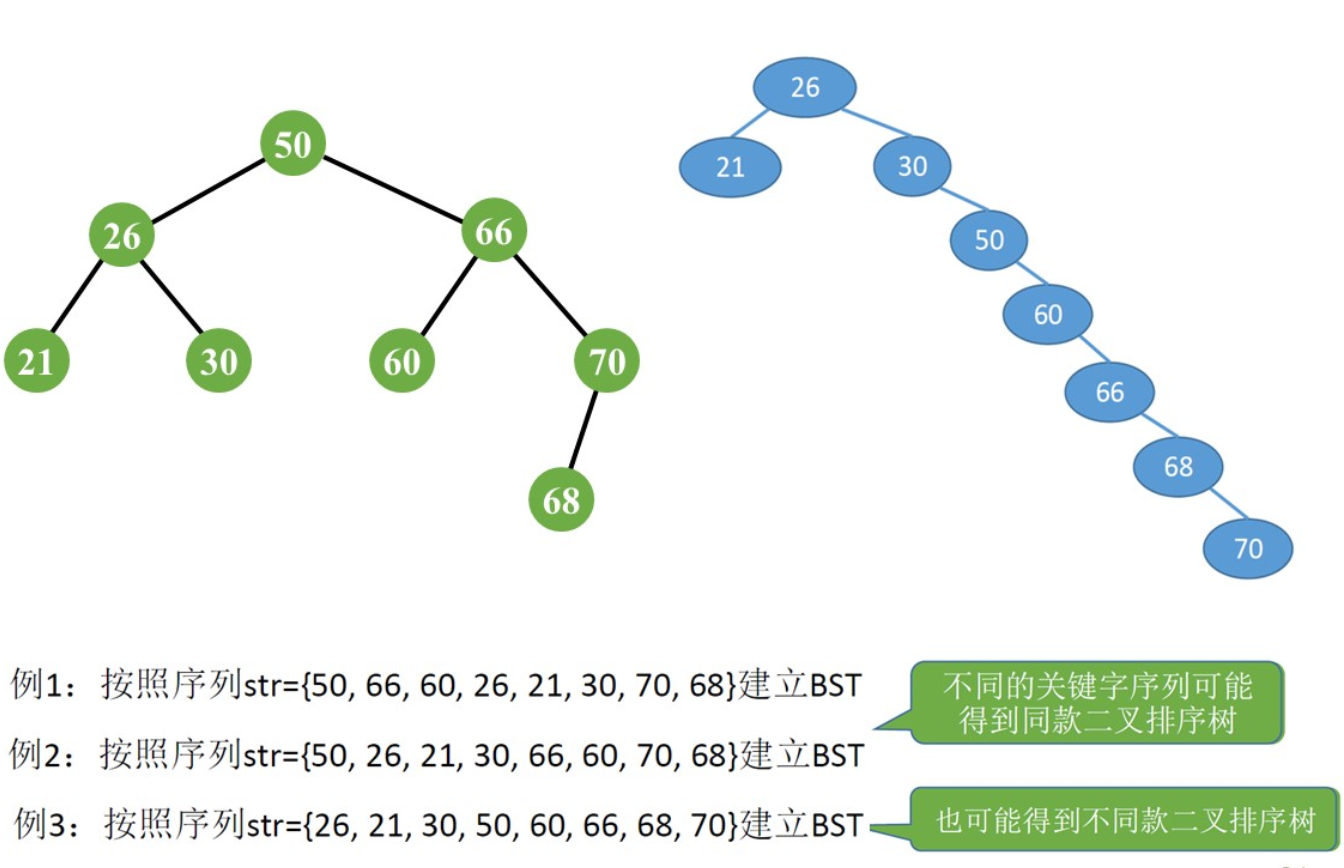
alt text

不同的关键字序列可能得到同款二叉排序树，也可能得到不同款

插入和查找

效率在平衡情况下是$O(log_2n)$，极端情况下退化为$O(n)$

删除

  • 如果是叶子节点，直接删除
  • 如果只有单左或单右子树，直接让子树代替
  • 如果有左、右两棵子树，则令直接后继(或直接前驱)替代，然后从二叉排序树中删去这个直接后继(或直接前驱)，这样就转换成了第一或第二种情况

平衡二叉树

平衡因子：左子树高-右子树高
使得效率不会退化为$O(n)$

判断失衡类型和对应调整方法

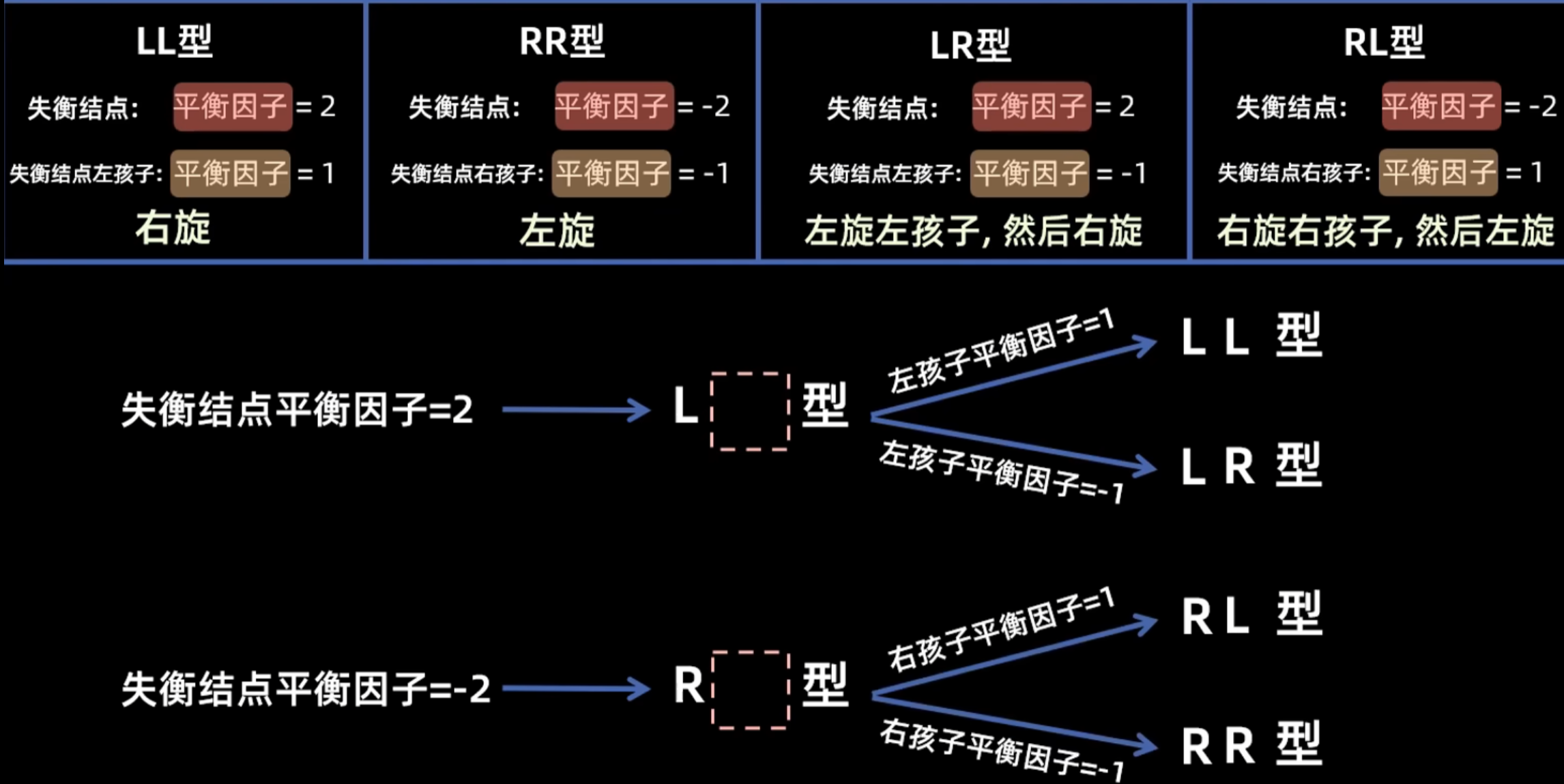
alt text

插入结点后如果导致多个祖先结点失衡只需调整距离插入结点最近的失衡结点，其他失衡结点会自然平衡

并查集

根节点指向自己

并查集的查找和路径压缩

alt text

路径压缩：各个节点直接指向根节点
递归的过程中赋值
alt text

合并

按秩合并：包括按高度和按大小

树越矮并查集效率越高

散列表（哈希表）

通过散列函数建立“关键字”与“存储地址”的关系
用空间换时间，将时间复杂度降到常数级别
是否“冲突”与散列函数的选取和装填因子有关

散列函数

  1. 乘法散列函数
    归一化后乘上一个常数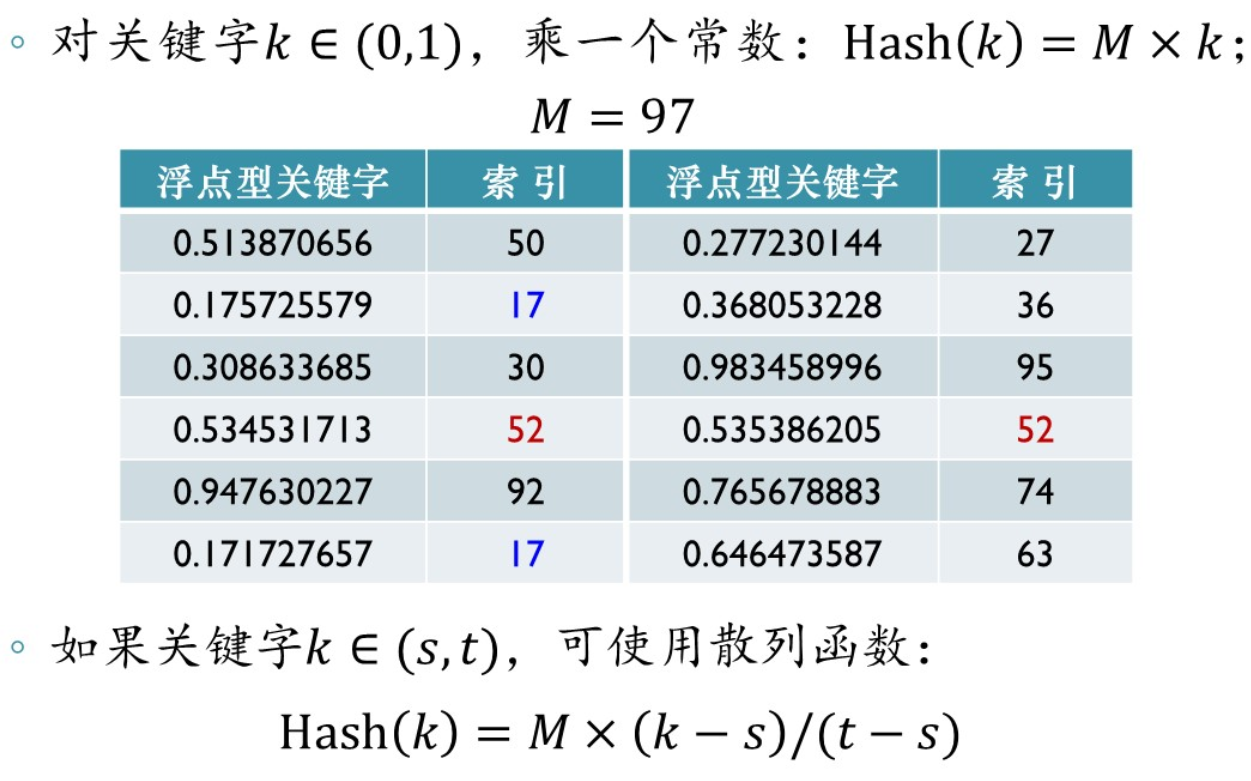
    alt text
  2. 模散列函数（除留余数法）
    质数因子一般选表长-1
    alt text
  3. 数学分析法
    …

装填因子

装填因子越大，冲突的可能性越大
装填因子越小，冲突的可能性越小，但是空间利用率越低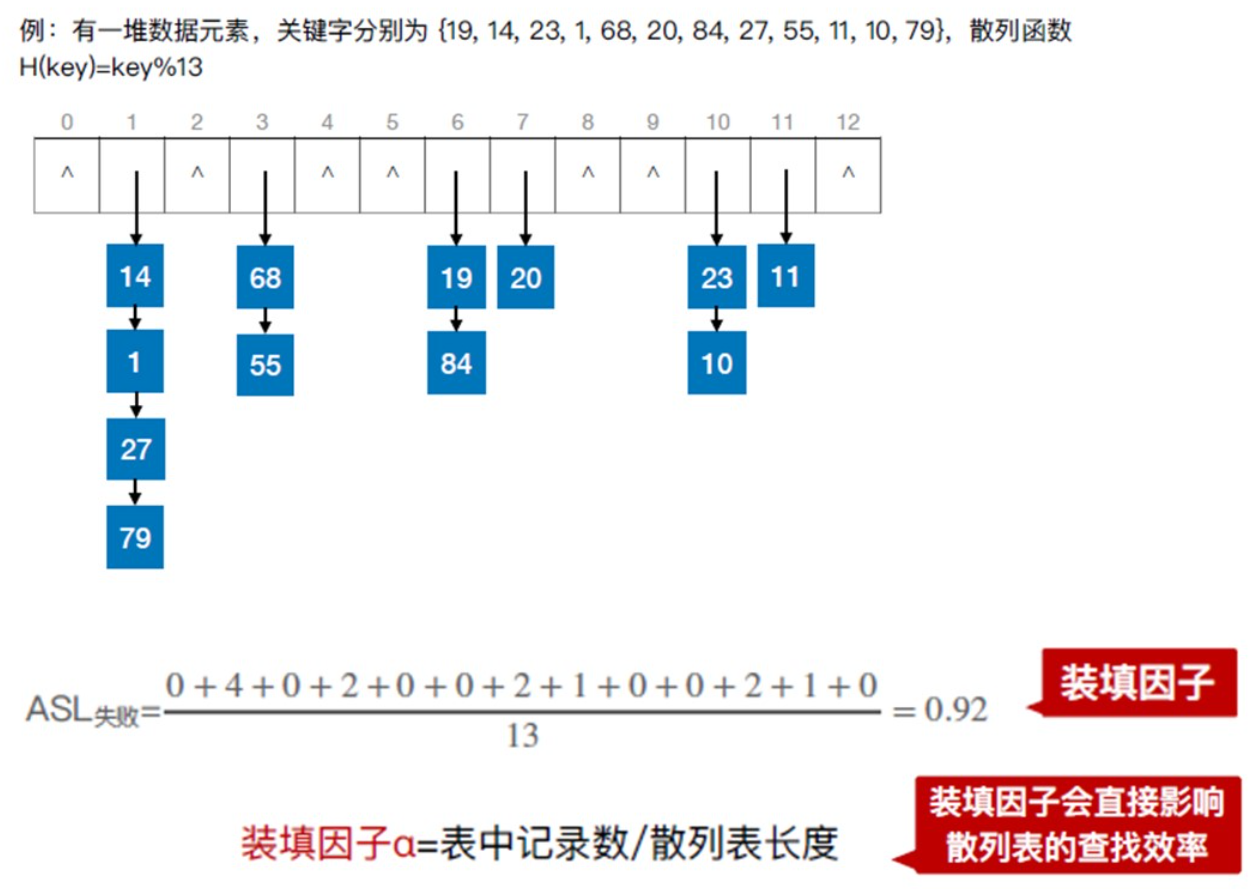
alt text

处理冲突的方法

  1. 拉链法
    链表存储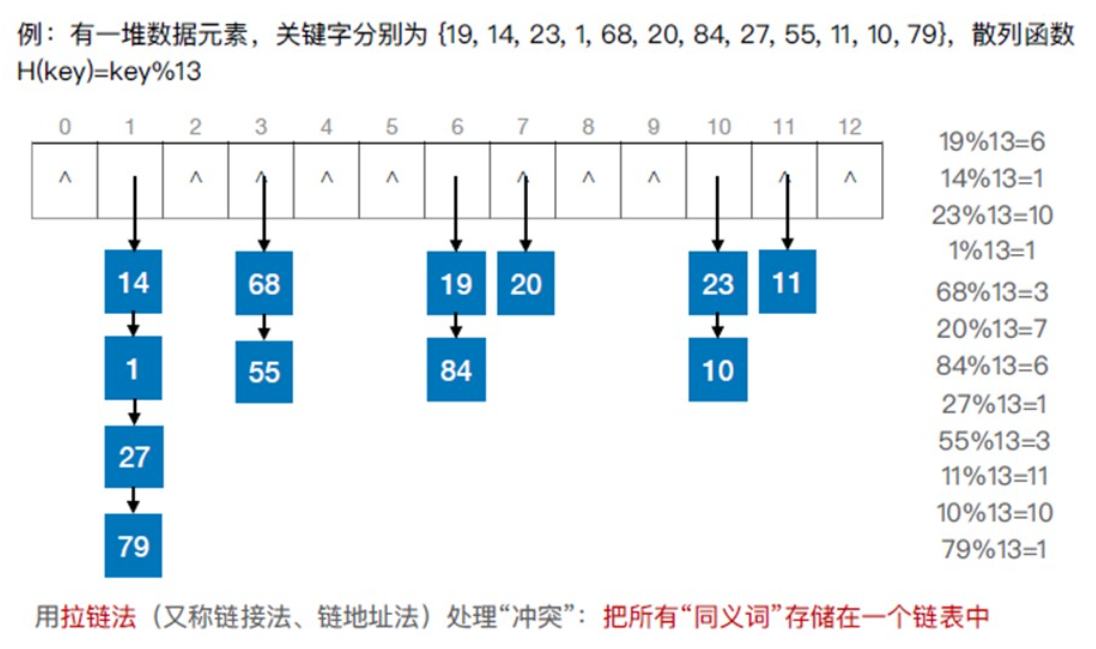
    alt text

ASL计算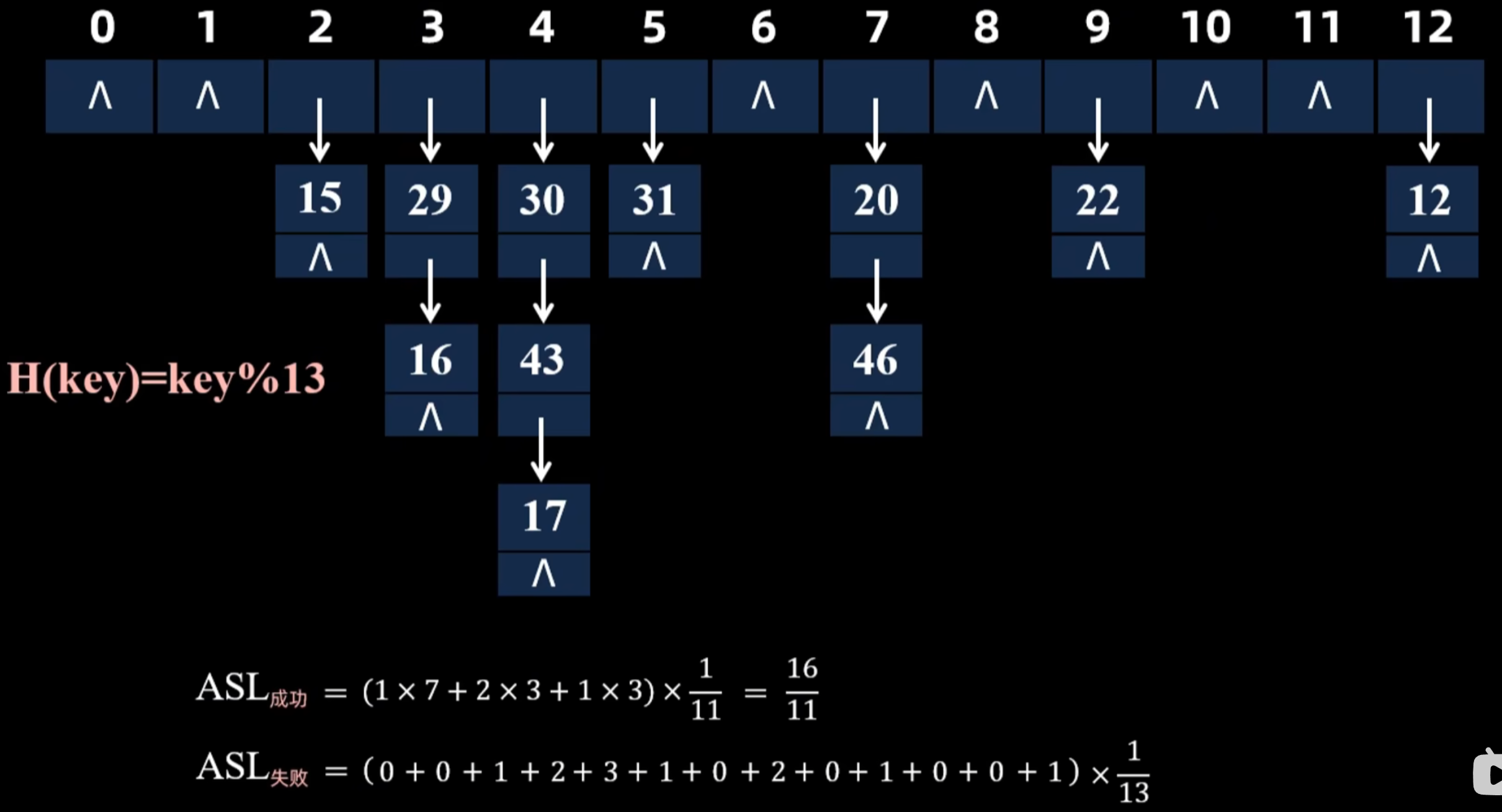
alt text

  1. 各种探测法
    alt text