数值计算
数值计算
近似与误差
误差
绝对误差 = 近似值 - 真值
- 精确度:近似某个量时有效数字的位数
- 精度:表示数的数字个数(不一定都是有效数字)
相对误差 = 绝对误差 / 真值(真值 ≠ 0)
近似值 = 真值 x (1 + 相对误差)
相对误差限 = 绝对误差限 / 近似值
计算过程中误差可能传递、积累或者是对消
有效数字
相对误差
例题:
误差来源
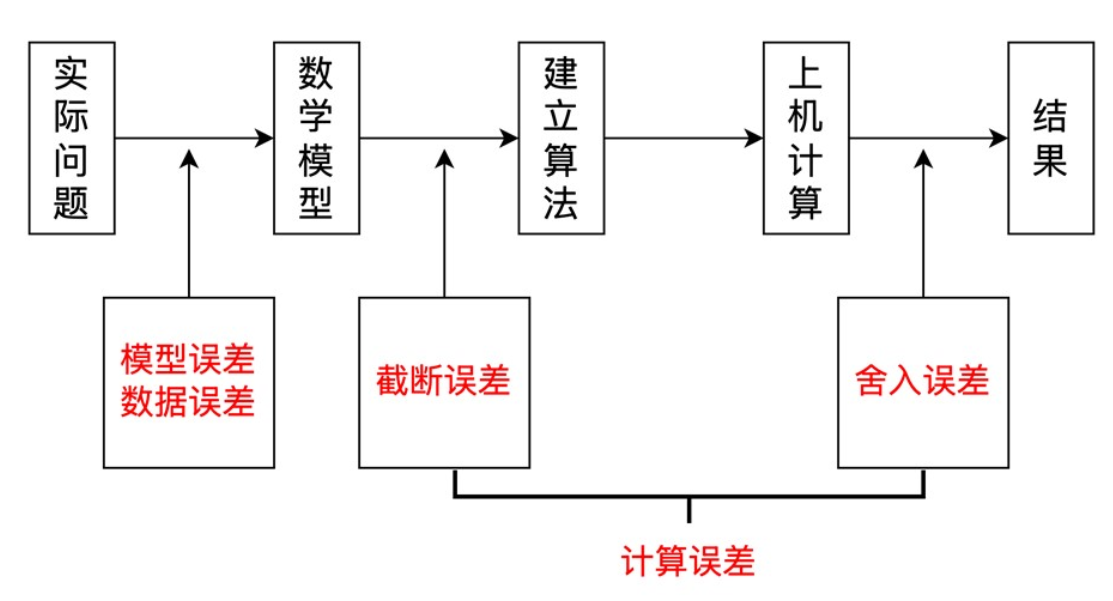
数据误差和计算误差
计算误差是在输入有误差的情况下产生的(因为因为误差是必然的),数据误差是在算法无误差的情况下产生的
计算误差包括截断误差和舍入误差

有限次求解的纯代数问题中,舍入误差主导;
涉及积分、导数、非线性等无限求解的问题,截断误差主导
向前误差与向后误差
向前误差:计算值与真值之间的偏差,通常比较难以估计
向后误差:输入数据有多大误差才能产生最终的计算值
若问题的近似解是其”邻近”问题的精确解(向后误差小),则认为近似是好的
例题:
敏感性和病态性
良态/不敏感: 在假设计算过程完全精确的前提下,如果输入数据的相对变化对于解的变化影响不大,就称问题是不敏感或良态的;
病态/敏感: 如果解的相对变化程度远超输入数据的变化,就称问题是敏感或者病态的
敏感性定量分析:条件数
对于可微函数求值问题:
对良态问题采用稳定的算法才会得到精确的解
计算机运算
浮点数

计算机中符号、指数、尾数均存储于定长的单独域中
零可以用尾数和指数都为零的浮点数表示
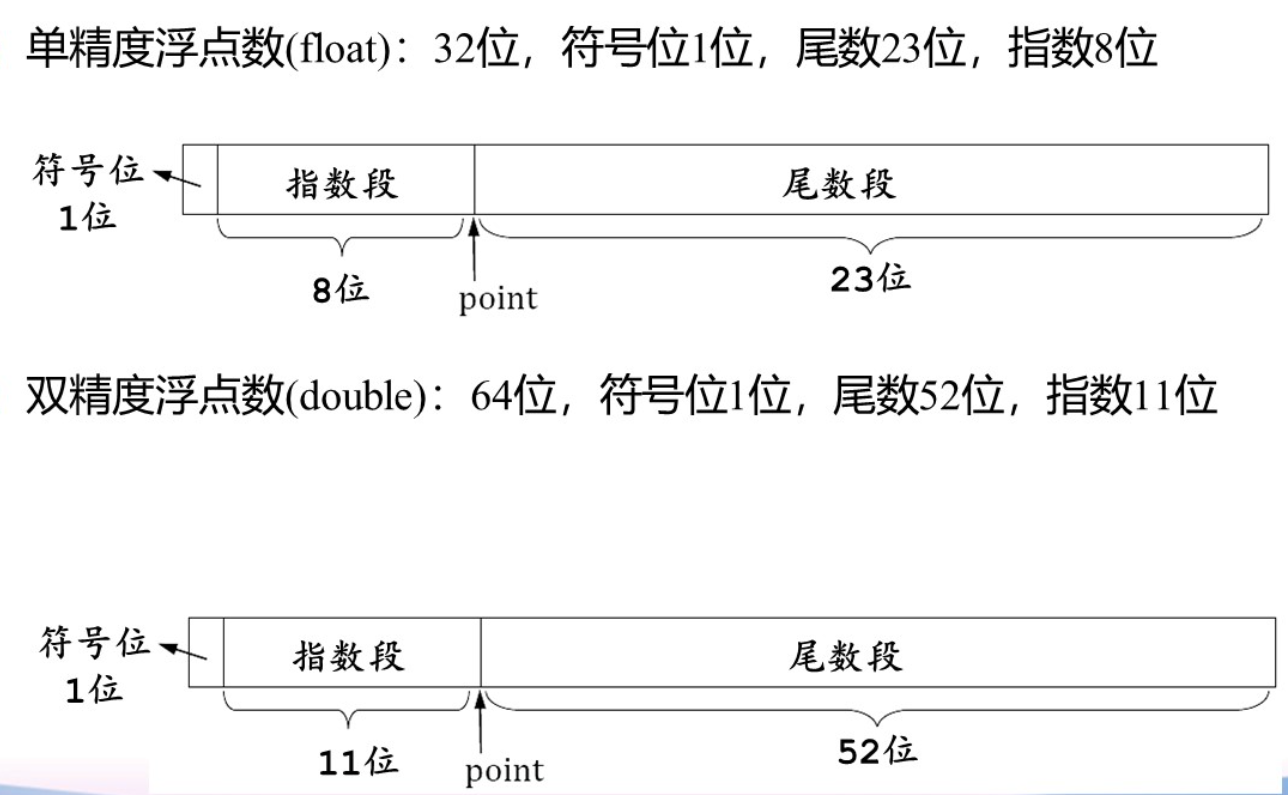
IEEE的单精度(32)与双精度(64)二进制浮点数应用最为广泛
IEEE标准浮点数系统
正规化
首位的限制(β-1种选择)
正规化条件:要求尾数 m 的首位数字满足 1 ≤ m < β(即小数点后第一个有效数字不能为0)
例子:
十进制(β=10):首位可以是 1-9(9种)
二进制(β=2):首位只能是 1(1种,因此二进制正规化浮点数会隐含存储首位)
其余位的自由(β种选择)
精度最大化:除首位的其他 p-1 位允许数字 0 到 β-1(共 β 种选择)
原因:
首位已保证唯一性,后续位的自由度不影响唯一性
允许后续位包含 0,可表示更精细的小数(如 1.023 比 1.23 精度更高)
在正规化浮点系统中,U 和 L 分别表示 指数部分(阶码)的允许取值范围的上限和下限,即:
- L(Lower Bound):指数的最小值(最小阶码)
- U(Upper Bound):指数的最大值(最大阶码)
为什么是“指数”的上下限?
浮点数总个数公式:
${2(\beta - 1)\beta^{p-1}(U - L + 1) + 1}$
${U - L + 1}$ 表示指数可能的取值总数(例如,若 ${L=-5}$, ${U=10}$,则共有 ${10 - (-5) + 1 = 16}$ 种指数值)。
该部分直接影响浮点数的“覆盖范围”,指数范围越大,可表示的数越广。最小正数(UFL)和最大正数(OFL)的公式:
${UFL = \beta^L}$:最小正数由最小指数 ${L}$ 决定(例如,${L=-126}$ 对应最小正规化数 ${2^{-126}}$)。
${OFL = \beta^{U+1}(1 - \beta^{-p})}$:最大正数由最大指数 ${U}$ 和尾数精度 ${p}$ 共同决定(例如,${U=127}$ 对应 ${2^{128}(1 - 2^{-24})}$)。
进一步说明
指数的作用:
浮点数 ${x}$ 可表示为:
${
x = \pm \left( d_0 + \frac{d_1}{\beta} + \cdots + \frac{d_{p-1}}{\beta^{p-1}} \right) \times \beta^e
}$
其中 ${e}$ 为指数(阶码),取值范围为 ${L \leq e \leq U}$。二进制特例:
二进制(${\beta=2}$)中,尾数首位 ${d_0}$ 固定为 1 ,但指数范围 ${L}$ 和 ${U}$ 仍然独立定义数值的尺度(如 IEEE 754 单精度浮点数中 ${L=-126}$, ${U=127}$)。
超过OFL,或是小于UFL的数均不能表示;在表示范围内,浮点数并非均匀分布
舍入
截断:即向零舍入
最近舍入:取与x最接近的浮点数,相等时选取最未存储位为偶数的浮点数(精确但代价高)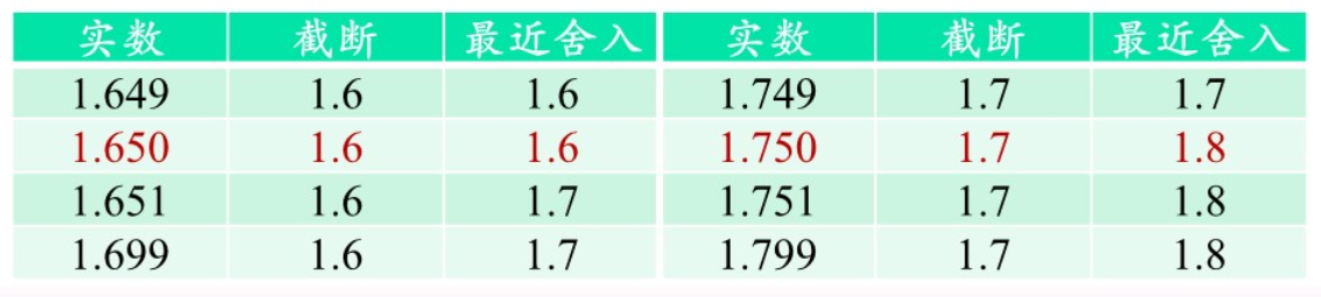
机器精度

机器精度由尾数的位数决定,下溢限由指数域的尾数决定,两者的定义不同
特殊值

浮点运算
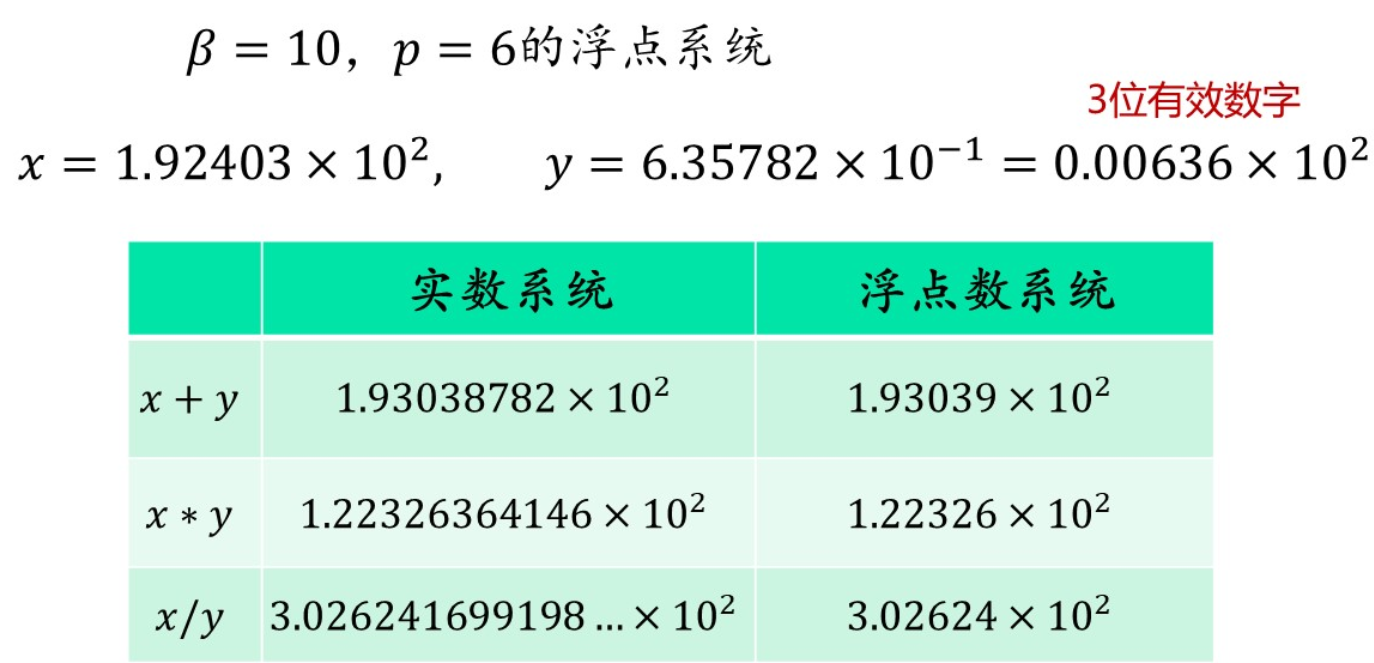
一般的,浮点数运算结果与对应实数运算结果不同
当计算结果超出浮点系统范围时,也不能表示(上溢和下溢),下溢可以当做零,但上溢往往是严重错误
例题:
某些实数域上的运算定律在浮点数集合中不满足
右侧计算:$(1+ϵ)+ϵ$
$1+ϵ$ 会因 $ϵ<ϵ_{mach}$而被舍入为 1;
再与 $ϵ$ 相加时,结果为 $1+ϵ$,仍被舍入为 1。
核心原因:
舍入规则:当中间结果的小数部分超出尾数精度 $p$ 时,必须舍入。
阈值差异:$2ϵ$ 可能跨越 $ϵ_{mach}$,从而在后续加法中保留;单次 $ϵ$ 因小于 $ϵ_{mach}$被直接丢弃。
“分配律”违背的原因也类似
总之,根本限制是浮点数的有限尾数位数 p 和固定基数 β 导致:
数值表示范围受限;
运算中超出精度的部分必须舍入,误差不可逆累积;
不同运算顺序可能触发不同次数的舍入,最终结果不同。
调和级数在实数域发散浮点数系统中直接运算,调和级数收敛
抵消

例题:
总结:通过选择其他公式避免原公式在计算时因为相近的数相减导致的“抵消”现象,可以避免最终的根非常接近